
1.已知定点F1、F2,且|F1F2|=6,动点P满足|PF1|-|PF2|=6,则动点P的轨迹是 ( )
A. 椭圆 B. 双曲线 C. 线段 D. 射线
21.(本题满分12分)
如图,已知抛物线 和直线
和直线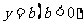 ,点
,点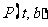 在直线
在直线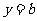 上移动,过点
上移动,过点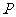 作抛物线的两条切线,切点分别为
作抛物线的两条切线,切点分别为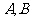 ,线段
,线段 的中点为
的中点为
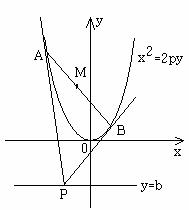
(1)设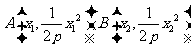 ,分别用
,分别用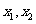 表示切线
表示切线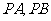 的斜率
的斜率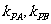 ;
;
(2)证明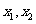 为方程
为方程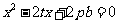 的两根,并求线段
的两根,并求线段 长的最小值;
长的最小值;
(3)求证直线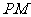 的倾斜角为定植,并求
的倾斜角为定植,并求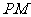 长的最小值。
长的最小值。
20.(本题满分12分)
一个口袋内装有大小相同的红色球和蓝色球共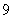 个,从中任取两个球,每个球被取出的机会都相同,且取得两球同色的概率为
个,从中任取两个球,每个球被取出的机会都相同,且取得两球同色的概率为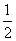
(1)求口袋内两种颜色的球相差多少个?
(2)如果每次从袋中取出一个球,辨认颜色后放回袋中,连续三次取出红色球就停止,否则继续取球,当口袋内红色球个数少于蓝色球个数时,求至多取六次就停止的概率。
18.(本题满分12分)
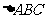 中,内角
中,内角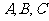 的对边分别是
的对边分别是 ,已知
,已知 成等差数列,且
成等差数列,且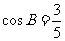
(1)求 和
和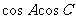 ;
;
(2)求 值。
值。
(3)判断等式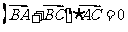 能不能成立?如果能,请求出的
能不能成立?如果能,请求出的 的一组值;如果不能,请说明理由。
的一组值;如果不能,请说明理由。
17.(本题满分12分)
已知函数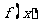 是定义在区间
是定义在区间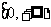 上的增函数,当
上的增函数,当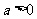 且
且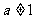 时,解关于
时,解关于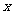 的不等式:
的不等式:
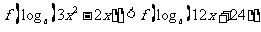
16、将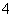 封不同的信投入
封不同的信投入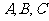 三个信箱中,每个信箱都不同,则共有________种不同的投入方法(用数字作答).
三个信箱中,每个信箱都不同,则共有________种不同的投入方法(用数字作答).
15、抛物线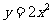 上的点与直线
上的点与直线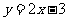 上的点之间距离的最小值为________.
上的点之间距离的最小值为________.
14、在四面体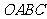 中,
中,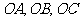 两两垂直,且
两两垂直,且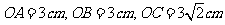 ,则四面体
,则四面体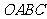 的外接圆的体积为_____________.
的外接圆的体积为_____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com