
26.(本小题为选做题,满分8分)
用数学归纳法证明不等式: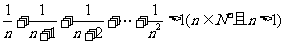 .
.
25.(本小题为选做题,满分8分)
试求曲线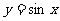 在矩阵MN变换下的函数解析式,其中M =
在矩阵MN变换下的函数解析式,其中M = ,N =
,N = .
.
24.(本小题为选做题,满分8分)
已知直线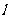 的参数方程:
的参数方程: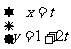 (
(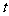 为参数)和圆
为参数)和圆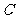 的极坐标方程:
的极坐标方程:
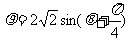 .
.
(1)将直线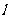 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆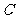 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)判断直线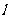 和圆
和圆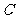 的位置关系.
的位置关系.
22.(本小题为必做题,满分12分)
甲、乙、丙三个同学一起参加某高校组织的自主招生考试,考试分笔试和面试两部分,笔试和面试均合格者将成为该高校的预录取生(可在高考中加分录取),两次考试过程相互独立.根据甲、乙、丙三个同学的平时成绩分析,甲、乙、丙三个同学能通过笔试的概率分别是0.6,0.5,0.4,能通过面试的概率分别是0.5,0.6,0.75.
(1)求甲、乙、丙三个同学中恰有一人通过笔试的概率;
(2)设经过两次考试后,能被该高校预录取的人数为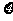 ,求随机变量
,求随机变量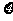 的期望
的期望 .
.
20.(本小题满分18分)
已知数列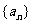 的通项公式是
的通项公式是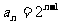 ,数列
,数列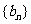 是等差数列,令集合
是等差数列,令集合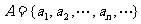 ,
,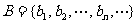 ,
,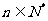 .将集合
.将集合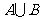 中的元素按从小到大的顺序排列构成的数列记为
中的元素按从小到大的顺序排列构成的数列记为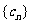 .
.
(1)若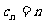 ,
,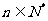 ,求数列
,求数列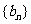 的通项公式;
的通项公式;
(2)若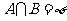 ,数列
,数列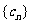 的前5项成等比数列,且
的前5项成等比数列,且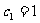 ,
,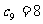 ,求满足
,求满足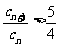
的正整数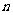 的个数.
的个数.
B.附加题部分
19.(本小题满分16分)
已知函数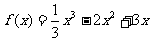 (
(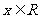 )的图象为曲线
)的图象为曲线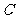 .
.
(1)求曲线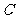 上任意一点处的切线的斜率的取值范围;
上任意一点处的切线的斜率的取值范围;
(2)若曲线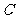 上存在两点处的切线互相垂直,求其中一条切线与曲线
上存在两点处的切线互相垂直,求其中一条切线与曲线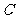 的切点的横坐标的取值范围;
的切点的横坐标的取值范围;
(3)试问:是否存在一条直线与曲线C同时切于两个不同点?如果存在,求出符合条件的所有直线方程;若不存在,说明理由.
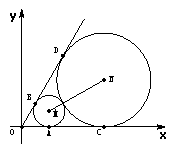
17.(本小题满分14分)
如图,已知圆心坐标为 的圆
的圆 与
与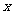 轴及直线
轴及直线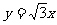 分别相切于
分别相切于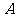 、
、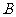 两点,另一圆
两点,另一圆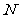 与圆
与圆 外切、且与
外切、且与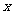 轴及直线
轴及直线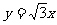 分别相切于
分别相切于 、
、 两点.
两点.
(1)求圆 和圆
和圆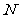 的方程;
的方程;
(2)过点B作直线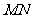 的平行线
的平行线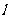 ,求直线
,求直线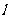 被圆
被圆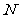 截得的弦的长度.
截得的弦的长度.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com