
6.函数f(x)=x+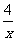 +3在(-∞,-2)上 ( )
+3在(-∞,-2)上 ( )
A.无最大值,有最小值7 B.无最大值,有最小值-1
C.有最大值7,有最小值-1 D.有最大值-1,无最小值
5.已知命题: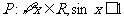 ,则 ( )
,则 ( )
A.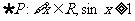 B.
B.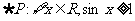

C.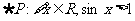 D.
D.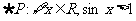
4.已知0>a>b,c>d>0,则下列不等式一定成立的是 ( )
A.ac>bd B.a-c>b-d C.a2>d2 D.c2>d2
3.与椭圆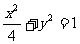 共焦点且过点Q(2,1)的双曲线方程是 ( )
共焦点且过点Q(2,1)的双曲线方程是 ( )
A.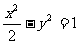 B.
B.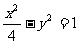
C.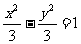 D.
D.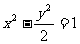
2.如果a,b,c都是实数,那么P∶ac<0,是q∶关于x的方程ax2+bx+c=0有一个正根和一个负根的 ( )
A.必要而不充分条件 B.充要条件
C.充分而不必要条件 D.既不充分也不必要条件
1.抛物线y2=6x的准线方程是 ( )
A.x=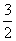 B.x+
B.x+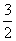 =0 C.y=
=0 C.y=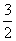 D.y+
D.y+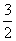 =0
=0
22.(9分)
抛物线y2=4px(p>0)的准线与x轴交于M点,过点M作直线l交抛物线于A、B两点.
(1)若线段AB的垂直平分线交x轴于N(x0,0),求证:x0>3p;
(2)若直线l的斜率依次为p,p2,p3,…,线段AB的垂直平分线与x轴的交点依次为N1,N2,N3,…,当0<p<1时,求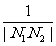 +
+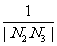 +…+
+…+ 的值.
的值.
21.(9分)
某单位准备建造一间占地面积为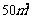 的背面靠墙的矩形平顶房屋,房屋墙的高度为4m,房屋正面的造价为800元/m2,房屋的侧面的造价为600元/m2,屋顶的造价为1000元/m2.若不计房屋背面的费用,问怎样设计房屋能使造价最底,最低造价是多少元?
的背面靠墙的矩形平顶房屋,房屋墙的高度为4m,房屋正面的造价为800元/m2,房屋的侧面的造价为600元/m2,屋顶的造价为1000元/m2.若不计房屋背面的费用,问怎样设计房屋能使造价最底,最低造价是多少元?
20.(12分)
如图,在长方体ABCD-A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AB上移动.
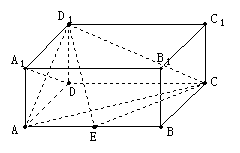
(1)证明:D1E⊥A1D;;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1-EC-D的大小为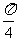 .
.
19.(9分)
已知A(0,-5),B(3,7),求抛物线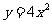 上的点到直线AB的最短距离,并求该点的坐标。
上的点到直线AB的最短距离,并求该点的坐标。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com