
2.已知等差数列{an}中,a6+a10=20,a4=2,则a12的值是 ( )
A.26 B.20 C.18 D.28
1.已知全集U=Z,A={-1,0,1,2},B= ( )
( )
A.{-1,2} B.{-1,0} C.{0,1} D.{1,2}
22.(本小题满分14分)
已知:三次函数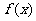 =x3+ax2+bx+c,在(-∞,-1),(2,+∞)上单调递增,在(-l,2)上单调递减,不等式
=x3+ax2+bx+c,在(-∞,-1),(2,+∞)上单调递增,在(-l,2)上单调递减,不等式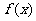 >x2-4x+5的解集为(4,+∞)
>x2-4x+5的解集为(4,+∞)
(I)求函数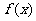 的解析式;
的解析式;

(II)若函数 =
= - (m+1)ln (x+m),求
- (m+1)ln (x+m),求 的单调区间.
的单调区间.
21.(本小题满分12分)
如图,F1,F2分别是椭圆 (a>b>0)的左右焦点,M为椭圆上一点, MF2垂直于x轴,且OM与椭圆长轴和短轴端点的连线AB平行,
(a>b>0)的左右焦点,M为椭圆上一点, MF2垂直于x轴,且OM与椭圆长轴和短轴端点的连线AB平行,
(I)求椭圆的离心率;
(II)若G为椭圆上不同于长轴端点任一点,求∠F1GF2的取值范围;
(Ⅲ)过F2且与OM垂直的直线交椭圆于P,Q两点. 若 =20,求椭圆的方程.
=20,求椭圆的方程.

20.(本题满分12分)
一群猴子第一天摘下若干个桃子,当即吃了,还不过瘾,又吃了两个. 第二天早上又将剩下的桃子吃掉,又吃了两个. 以后每天早上都吃掉前一天剩下的后还要吃两个. 到第七天早上想吃时,只剩下一个桃子了,求第一天共摘了多少个桃子?
19.(本题满分l2分)
在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为x、y,记ξ=|x一2| +| y一x|.
(I)求随机变量ξ 的最小值,并求事件“ξ 取得最小值”的概率;
(Ⅱ)求随机变量ξ 的分布列和数学期望.
18.(本题满分12分)
已知在等比数列{an}中,al+a3=l0,a2+a4=20,设cn=11一log2 a2n.
(I)求数列{cn}的通项;
(Ⅱ)求数列{cn}前n项和Sn的最大值.
17.(本题满分l2分)
在ΔABC中,角A、B、C的对边分别为a、b、c,4cos2 一cos2C =,a+b=5,c=
一cos2C =,a+b=5,c= .
.
(1)求角C的大小;
(2)求ΔABC的面积.
16.用n个不同的实数a1,a2,…,an可得到n!个不同的排列,每个排列为一行写成一个n!行的数阵. 对第i行ai1,ai2,…,ain ,记b1= 一ai1+2ai2 -3ai3+…+(一1)n n ain,i=l,2,3,…,n!. 例如1,2,3可得数阵如图,由于此数阵中每一列各数之和都是l2,所以bl+b2+…+b6=一l2 +2×12-3×12=一24,那么,在用l,2,3,4,5形成的数阵中,bl +b2 +…+b120=______.
|

15.若对于任意实数x,有x3=a0+al(x一2)+a2(x一2)2+a3(x一2)3 ,则a2=_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com