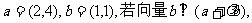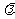1．已知向量则实数的值是　　　　　 。

20．数列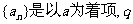为公比的等比数列，令

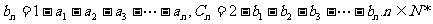
　 (1)试用a,q表示b_n和c_n；

　 (2)若a<0，q>0且q≠1，试比较c_n与c­_n+1的大小；

　 (3)是否存在实数对(a,q)，其中q≠1,使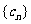成等比数列，若存在，求出实数对(a,q)和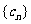的通项公式；若不存在，请说明理由。

19．已知函数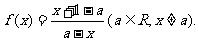

　 (1)证明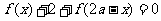：对定义域内的所有x都成立；

　 (2)当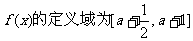时，求证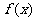的值域为[－3，－2]；

　 (3)设函数的最小值。

0.99²≈0.98,　 0.99²≈0.97, 0.99⁴≈0.96,　 0.99⁵≈0.95,　 0.99⁶≈0.94, 0.99⁷≈0.93.

18．某国由于可耕地面积少，计划从今年起的五年填湖围造一部分生产和生活用地，若填湖费、购置排水设备费等所需经费与当年所填湖造地面积x(亩)的平方成正比，其比例系数为a，设每亩水面的年平均经济效益为b元，填湖造地后的每亩土地的年平均收益为c元(其中a，b，c均为常数)。

　 (1)若按计划填湖造地，且使得今年的收益不小于支出，试求所填面积x的最大值。

　 (2)如果填湖造地面积按每年1%的速度减少，为保证水面的畜洪能力和环保要求，填湖造地的总面积不能超过现有水面面积的25%，求今年填湖造地的面积最多只能占现有水面的百分之几。

注：根据下列近似值进行计算：

17．曲线C上任意一点到E(－4，0)，F(4，0)的距离的和为12，C与x轴的负半轴、正半轴依次交于A、B两点，点P在C上，且位于x轴上方，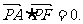

　 (1)求曲线C的方程；

　 (2)求点P的坐标；

　 (3)求曲线C的中心为圆心，AB为直径作圆O，过点P的直线l截圆O的弦MN长为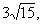求直线l的方程。

16．已知函数的图象在点P(2，f(2))处的切线方程为

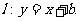
　 (1)求出函数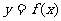的表达式和切线l方程；

　 (2)当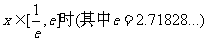，不等式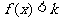恒成立，求实数k的取值范围。

15．在△ABC中，三个内角是A，B，C的对边分别是a,b,c，其中c=10，且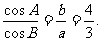

　 (2)设圆O过A，B，C三点，点P位于劣弧AC上，∠PAB=60°，求四边形ABCP的面积。

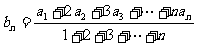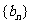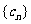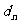14．数列是正项等差数列，若，则数列也为等差数列，类比上述结论，写出正项等比数列，若=　　　　　　　 ，则数列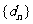也为等比数列。

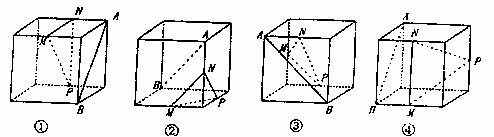
13．下列四个正方体中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出AB//MNP的图形的序号是　　　　　　　 (写出所有符合要求的图形序号)