
5.在锐角△ABC中,若lg (1+sinA) = m , 且lg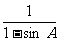 = n,则lgcosA等于 ( )
= n,则lgcosA等于 ( )
A.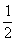 (m-n) B.m-n C.
(m-n) B.m-n C.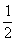 ( m+
( m+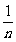 ) D.m+
) D.m+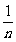
4.如图,已知单位圆O与y轴相交于A、B两点.角θ的顶点为原点,始边在x轴的正半轴上,终边在射线OC上. 过点A作直线AC垂直于y轴且与角θ的终边交于点C,则有向线段AC的函数值是 ( )
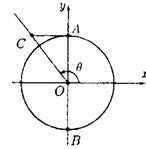
A.sinθ B. cosθ
C.tanθ D. cotθ
3.数据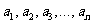 的方差为
的方差为 ,则数据
,则数据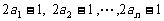 的方差为 ( )
的方差为 ( )
A.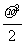 B.
B.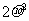 -1 C.
-1 C. 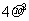 D.
D.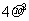 -1
-1
2.已知复数z = (2 + 3i)( 1 – 4i ) , 则z在复平面上对应的点Z位于 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
1.若集合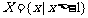 ,则下列关系成立的是 ( )
,则下列关系成立的是 ( )
A.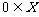 B.
B. 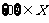 C.
C.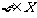 D.
D. 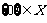
(17)(本小题满分12分)
在△ABC中,角A、B、C的对边分别是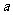 、
、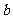 、
、 ,且角A为锐角,
,且角A为锐角,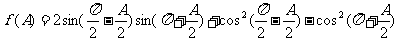
(I)求 的最小值;
的最小值;
(Ⅱ)若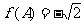 ,
,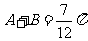 ,
,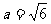 ,求
,求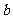 的大小。
的大小。
(18)(本小题满分12分)
已知函数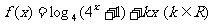 是偶函数。
是偶函数。
(I)求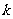 的值;
的值;
(II)若方程 有解,求
有解,求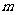 的取值范围。
的取值范围。
(19)(本小题满分12分)
如图,直四棱柱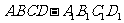 中,侧棱
中,侧棱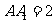 ,底面ABCD是菱形,AB=2,
,底面ABCD是菱形,AB=2,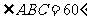 ,P为侧棱
,P为侧棱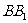 上的动点.
上的动点.
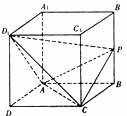
(I)求证: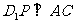 ;
;
(Ⅱ)当P恰为棱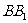 的中点时,求四面体CPDlA的体积。
的中点时,求四面体CPDlA的体积。
(20)(本小题满分12分)
2008年奥运会在中国召开,某商场预计2008年从1月份起前 个月,顾客对某种奥运商品的需求总量
个月,顾客对某种奥运商品的需求总量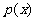 件与月份
件与月份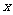 的近似关系是
的近似关系是
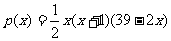 ,
,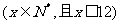
该商品的进价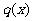 元与月份
元与月份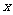 的近似关系是
的近似关系是
 ,
,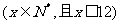
(I)写出今年第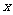 月的需求量
月的需求量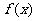 件与月份
件与月份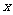 的函数关系式;
的函数关系式;
(Ⅱ)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,则此商场今年销售该商品的月利润预计最大是多少元?
(21)(本小题满分12分)
已知平面直角坐标系中,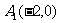 、
、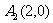 、
、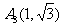 ,
,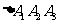 的外接圆为C;椭圆
的外接圆为C;椭圆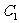 以线段
以线段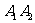 为长轴,离心率
为长轴,离心率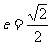 。
。
(I)求圆C及椭圆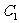 的方程;
的方程;
(Ⅱ)设椭圆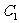 的右焦点为F,点P为圆C上异于A1、A2的动点,过原点O作直线PF的垂线交直线
的右焦点为F,点P为圆C上异于A1、A2的动点,过原点O作直线PF的垂线交直线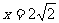 在手点Q,判断直线PQ与圆C的位置关系,并给出证明.
在手点Q,判断直线PQ与圆C的位置关系,并给出证明.
(22)(本小题满分14分)
已知二次函数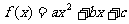 满足条件:
满足条件:
①0,1是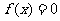 的两个零点;②
的两个零点;②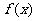 的最小值为
的最小值为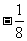 。
。
(I)求函数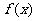 的解析式;
的解析式;
(Ⅱ)设数列{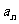 }的前
}的前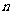 项积为
项积为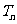 ,且
,且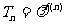 ,(
,(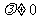 ,
,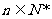 ),求数列{
),求数列{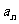 }的前
}的前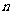 项和
项和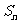 ;
;
(Ⅲ)在(Ⅱ)的条件下,当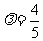 时,若
时,若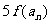 是
是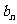 与
与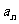 的等差中项,试问数列{
的等差中项,试问数列{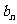 }中第几项的值最小?并求出这个最小值。
}中第几项的值最小?并求出这个最小值。
(13)已知双曲线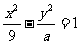 的右焦点为(
的右焦点为(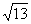 ,0),则该双曲线的渐近线方程为
。
,0),则该双曲线的渐近线方程为
。
(14)设等差数列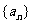 的前
的前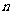 项和为
项和为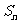 ,若
,若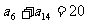 ,则
,则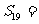 。
。
(15)已知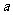 ,
,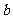 表示直线,
表示直线,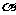 ,
,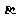 ,
,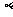 表示平面,结出下列条件:
表示平面,结出下列条件:
① ,
, ,
,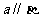 ,
,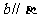 ; ②
; ②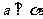 ,
, ,
,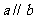 ;
;
③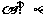 ,
,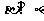 ; ④
; ④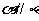 ,
, ;
;
其中能推出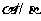 的是 (把所有正确的条件序号都填上)。
的是 (把所有正确的条件序号都填上)。
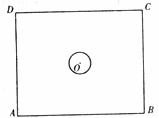
(16)如上图,平面上一长12cm,宽10cm的矩形ABCD内有一半径为1cm的圆O(圆心O在矩形对角线交点处),把一枚半径1cm的硬币任意掷在矩形内(硬币完全落在矩形内),则硬币不与圆D相碰的概率为 。
(1)若复数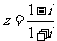 ,则
,则 等于
等于
(A) (B)
(B) (C)
(C)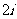 (D)
(D)
(2)甲、乙两名同学在5次体育测试中的成绩统计的茎叶图如图所示,若甲、乙两人的平均成绩分别是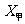 、
、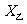 ,则下列结论正确的是
,则下列结论正确的是
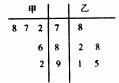
(A)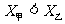 ;乙比甲成绩稳定 (B)
;乙比甲成绩稳定 (B) ;甲比乙成绩稳定
;甲比乙成绩稳定
(C) ;乙比甲成绩稳定 (D)
;乙比甲成绩稳定 (D)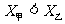 ;甲比乙成绩稳定
;甲比乙成绩稳定
(3)已知向量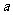 ,
,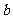 均为单位向量,若它们的夹角为60°,则
均为单位向量,若它们的夹角为60°,则 等于
等于
(A)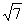 (B)
(B) (C)
(C)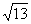 (D)4
(D)4
(4)在下列各函数中,最小值等于2的函数是
(A)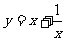 (B)
(B)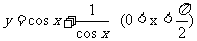
(C)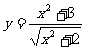 (D)
(D)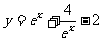
(5)已知圆O的方程是 ,过点M(3,0)的最短弦所在直线方程是
,过点M(3,0)的最短弦所在直线方程是
(A)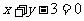 (B)
(B)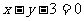
(C)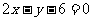 (D)
(D)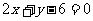
(6)如图所示的程序框图输出的结果是
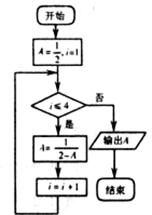
(A)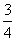 (B)
(B)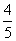 (C)
(C)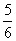 (D)
(D)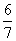
(7)用单位正方体搭成一个几何体,使它的主视图和俯视图如图所示,则符合条件的几何体体积的最小值与最大值分别是
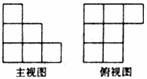
(A)9,13 (B)7,16 (C)10,15 (D)10,16
(8)已知函数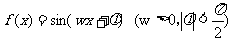 的最小正周期为
的最小正周期为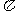 ,且其图像向左平移
,且其图像向左平移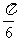 个单位后得到的函数为奇函数,则函数
个单位后得到的函数为奇函数,则函数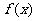 的图像
的图像
(A)关于点(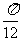 ,0)对称 (B)关于直线
,0)对称 (B)关于直线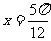 对称
对称
(C)关于点(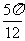 ,0)对称 (D)关于直线
,0)对称 (D)关于直线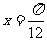 对称
对称
(9)函数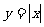 与
与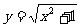 在同一坐标系中的图像可能是
在同一坐标系中的图像可能是
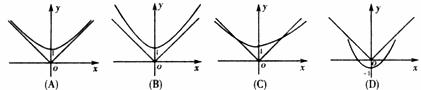
(10)抛物线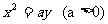 的准线
的准线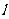 与
与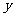 轴交于点P,若
轴交于点P,若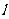 绕点P以每秒
绕点P以每秒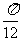 弧度的角速度按逆时针方向旋转
弧度的角速度按逆时针方向旋转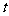 秒钟后,恰与抛物线第一次相切,则
秒钟后,恰与抛物线第一次相切,则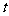 等于
等于
(A)1 (B)2 (C)3 (D)4
(11)古代“五行”学说认为:“物质分金、木、水、火、土五种属性,金克木,木克土,土克水,水克火,火克金”,从五种不同属性的物质中随机抽取两种,则抽取的两种物质不相克的概率是
(A)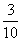 (B)
(B)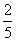 (C)
(C)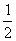 (D)
(D)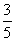
(12)函数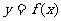 是定义在[
是定义在[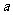 ,
,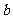 ]上的增函数,其中
]上的增函数,其中 ,且
,且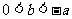 ,已知
,已知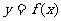 无零点。设函数
无零点。设函数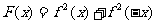 ,则对于
,则对于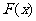 有如下四个说法:
有如下四个说法:
①定义域是[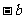 ,
,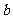 ];②是偶函数;③最小值是0;④在定义域内单调递增。
];②是偶函数;③最小值是0;④在定义域内单调递增。
其中正确说法的个数有
(A)4个 (B)3个 (C)2个 (D)1个
第Ⅱ卷 (非选择题 共90分)
22.(本小题满分14分)
已知函数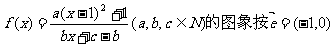 平移后得到的图象关于原点对称,
平移后得到的图象关于原点对称,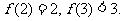
(1)求a,b,c的值;(2)设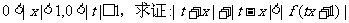 ;
;
(理科学生)(3)设x是正实数,求证: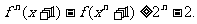
21.(本小题满分14分)
已知椭圆C的方程是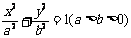 ,斜率为1的直线l与椭圆C交于
,斜率为1的直线l与椭圆C交于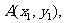
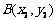 两点. (1)若椭圆的离心率
两点. (1)若椭圆的离心率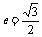 ,直线l过点M(b,0),且
,直线l过点M(b,0),且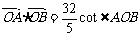 ,求椭圆的方程;(2)直线l过椭圆的右焦点F,设向量
,求椭圆的方程;(2)直线l过椭圆的右焦点F,设向量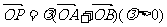 ,若点P在椭圆C上,求
,若点P在椭圆C上,求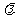 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com