
4.已知函数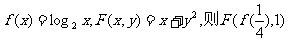 等于 ( )
等于 ( )
A.-1 B.5 C.-8 D.3
3.圆 的位置关系是( )
的位置关系是( )
A.外离 B.外切 C.相交 D.内含
2.已知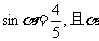 是第二象限角,那么
是第二象限角,那么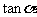 的值是 ( )
的值是 ( )
A.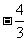 B.
B.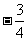 C.
C.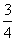 D.
D.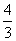
1.已知合集I={1,2,3,4,5,6},集合A={1,3,4,5},集合B={1,4}则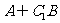 等 于 ( )
等 于 ( )
A.{1,4} B.{2,6} C.{3,5} D.{2,3,5,6}
22.(本小题满分14分)设函数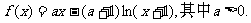
(1)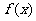 的单调区间;
的单调区间;
(2)当x>0时,证明不等式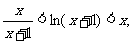
(3)设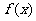 的最小值为
的最小值为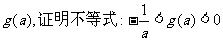
21.(本小题满分12分)已知定点A(-2,0),动点B是圆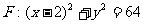 (F为圆心)上一点,线段AB的垂直平分线交BF与P。
(F为圆心)上一点,线段AB的垂直平分线交BF与P。
(1)求动点P的轨迹方程;
(2)是否存在过点E(-4,0)的直线l交P点于轨迹于点R,T,且满足
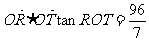 (O为原点),若存在,求直线l的方程,若不存在,请说明理由。
(O为原点),若存在,求直线l的方程,若不存在,请说明理由。
20.(本小题满分12分)
已知函数值不恒为0的单调函数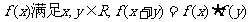 ,同时数列
,同时数列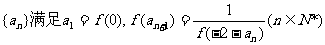
(1)求数列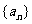 的前n项和Sn;
的前n项和Sn;
(2)令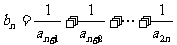 ,求数列bn的最小值。
,求数列bn的最小值。
19.(本小题满分12分)在中央电视台所举办的北京2008年奥运会火炬手的一期选拔节目中,假定每个选手需要进行四轮考核,每轮设有一个问题,能正确回答者进入下一轮考核,否则被淘汰,已知某选手能正确回答第一、二、三、四轮问题的概率分别为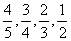 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。
(1)求该选手进入第四轮才被淘汰的概率;
(2)求该选手至多进入第三轮考核的概率;
(3)该选手在选拔过程中回答过的问题的总个数记为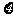 ,求随机变量
,求随机变量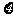 的分布列与数学期望。
的分布列与数学期望。
18.(本小题满分12分)如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC。
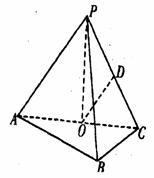
(1)求证:OD//平面PAB;
(2)当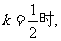 求直线PA与平面PBC所成角的正弦值;
求直线PA与平面PBC所成角的正弦值;
(3)当k取何值时,O在平面PBC内的射影恰好为△PBC的重心?
17.(本小题满分12分)若函数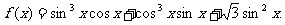
(1)求函数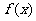 的单调递减区间;
的单调递减区间;
(2)已知△ABC的三边a、b、c对应角为A、B、C,且三角形的面积为S,若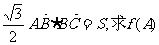 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com