

22.(本小题满分13分)设椭圆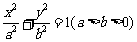 的左、右焦点分别为
的左、右焦点分别为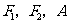 是椭圆上的一点,
是椭圆上的一点,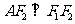 ,原点
,原点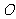 到直线
到直线 的距离为
的距离为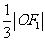 .
.
(Ⅰ)证明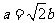 ;
;
(Ⅱ)求b为何值时,过圆 上一点M(2,
上一点M(2,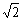 )处的切线交椭圆于
)处的切线交椭圆于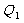 ,
,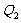 两点,而且
两点,而且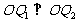 .
.
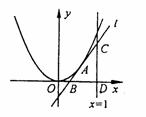
21.(本小题满分13分)抛物线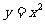 上有一点A(
上有一点A(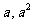 ),
),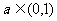 ,过点A引抛物线的切线
,过点A引抛物线的切线 分别交
分别交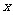 轴及直线
轴及直线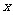 =1于B,C两点,直线
=1于B,C两点,直线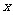 =1交
=1交 轴于D.
轴于D.
(1)求切线 的方程;
的方程;
(2)求图中∆BCD的面积S(a) ,并求出a为何值时S(a)有最大值 .
20.(本小题满分12分)在数列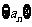 中,
中,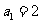 ,
,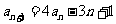 ,
,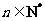 .
.
(Ⅰ)证明数列 是等比数列;
是等比数列;
(Ⅱ)求数列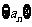 的前
的前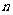 项和
项和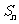 ;
;
|
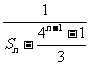 的前n项和,求Tn .
的前n项和,求Tn . 19.(本小题满分12分)右图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体, 截面为ABC. 已知A1B1=B1C1=l,∠AlBlC1=90°, AAl=4,BBl=2,CCl=3.
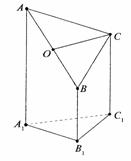
(1)设点O是AB的中点,证明:OC∥平面A1B1C1;
(2)求AB与平面AA1C1C所成的角的大小;
18.(本小题满分12分)栽培甲、乙两种果树,先要培育成苗,然后再进行移栽,已知甲、乙两种果树成苗的概率分别为0.6 ,0.5,移栽后成活的概率分别为0.7,0.9。
(1)求甲、乙两种果树至少有一种果树成苗的概率;
(2)求甲、乙两种果树分别能培育成苗且移栽成活的概率.
(3)求恰好有一种果树能培育成苗且移栽成活的概率.
17.(本小题满分12分)已知△ABC顶点所对边分别为a、b、c,且△ABC周长为
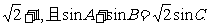
(Ⅰ)求边c的长;
(Ⅱ)若△ABC的面积为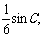 求角C的度数.
求角C的度数.
16.已知长方形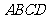 ,
,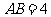 ,
,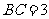 ,则以
,则以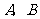 为焦点,且过
为焦点,且过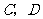 两点的椭圆的离心率为______.
两点的椭圆的离心率为______.
15.甲、乙两名射箭运动员在决定性测试中各射箭20次,两人的测试成绩如下表
|
甲的成绩 |
|
乙的成绩 |
||||||||||
|
环数 |
6 |
7 |
8 |
9 |
10 |
|
环数 |
6 |
7 |
8 |
9 |
10 |
|
频数 |
3 |
3 |
4 |
6 |
4 |
|
频数 |
4 |
4 |
4 |
4 |
4 |
那么应该选择、乙之中的(哪位) 运动员参加比赛更有优势.
14.若x、y是满足x+y=20的正数,则lgx+lgy 的最大值是 .
13.已知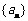 是等差数列,
是等差数列, ,其前5项和
,其前5项和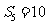 ,则其公差
,则其公差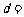 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com