20．(本小题满分12分)

已知函数．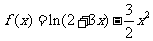

　 (1)求在[0，1]上的单调区间；

　 (2)若对任意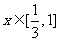，不等式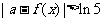，求实数a的取值范围．

19．(本小题满分12分)

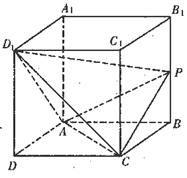
如图，直四棱柱ABCD-A₁B₂C₃D₄中，侧棱AA₁=2，底面ABCD是菱形，AB=2,∠ABC=60°，P为侧棱BB₁上的动点．

　 (1)求证：D₁P⊥AC；

　 (2)当二面角D₁-AC-P的大小为120°，求BP的长；

　 (3)在(2)的条件下，求三棱锥P-ACD₁的体积．

18．(本小题满分12分)

甲、乙两人参加某电视台举办的答题闯关游戏，按照规则，甲先从6道备选题中一次性抽取3道题独立作答，然后由乙回答剩余3题，每人答对其中2题就停止答题，即闯关成功．已知在6道被选题中，甲能答对其中的4道题，乙答对每道题的概率都是．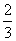

　 (1)求甲、乙至少有一人闯关成功的概率；

　 (2)设甲答对题目的个数为ξ₁，求ξ的分布列及数学期望．

17．(本小题满分12分)

在△ABC中，角A、B、C的对边分别是a、b、c，且A为锐角，

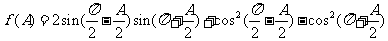
　 (1)求f(A)的最小值；

　 (2)若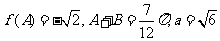，求b的大小．

16．如图，平面上一长12cm，宽10cm的矩形ABCD内有一半径为1cm的圆O(圆心O在矩形对角线交点处)．把一枚半径1cm的硬币任意掷在矩形内(硬币完全落在矩形内)，则硬币不与圆O相碰的概率为_________________．

15．二项式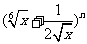展开式中，前三项系数依次组成等差

数列，则展开式中的常数项等于____________________．

14．设等差数列{a_n}的前n项和为S_n，若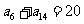，则S₁₉=______________．

13．已知双曲线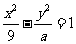的右焦点为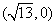，则该双曲线的渐近线方程为__________．

12．函数y=f(x)是定义在[a，b]上的增函数，期中a，b∈R，且0<b<-a，已知y=f(x)无零点，设函数F(x)=f²(x)+f²(-x)，则对于F(x)有如下四个说法：　　　　　　　　　　　　　　

①定义域是[-b，b]；　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　 ②是偶函数；　　

③最小值是0；　　　　 　　　　　　　　　　　　　　　　 ④在定义域内单调递增

其中正确的说汉的个数有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A．4个　　　　　　　　　　 B．3个　　　　　　　　　　 C．2个　　　　　　　　　　 D．1个

第Ⅱ卷(非选择题　 共90分)

11．抛物线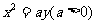的准线l与y轴交于点P，若l绕点P以每秒弧度的角速度按逆时针方向旋转t秒钟后，恰与抛物线第一次相切，则t等于　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A．1　　　　　　　　　　　　 B．2　　　　　　　　　　　　 C．3　　　　　　　　　　　　 D．4