
2.设全集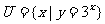 ,集合
,集合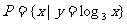 ,
, ,则
,则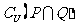 等于 ( )
等于 ( )
A. B.
B. C.
C. D.
D.
1.若复数 (其中
(其中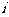 是虚数单位)的虚部是 ( )
是虚数单位)的虚部是 ( )
A.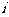 B.
B. C.1 D.
C.1 D.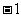
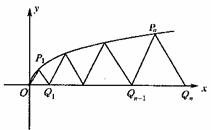
22.(本小题满分14分) 幂函数y = 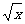 的图象上的点
Pn(tn2,tn)(n = 1,2,……)与
x 轴正半轴上的点
的图象上的点
Pn(tn2,tn)(n = 1,2,……)与
x 轴正半轴上的点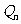 及原点 O 构成一系列正△Pn
及原点 O 构成一系列正△Pn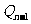
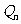 (
(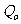 与O重合),记 an = |
与O重合),记 an = |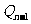
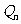 |
|
(Ⅰ)求 a1的值;
(Ⅱ)求数列 {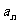 } 的通项公式
} 的通项公式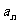 ;
;
(Ⅲ)设
Sn为数列 {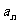 } 的前 n 项和,若对于任意的实数 l∈[0,1], 3Sn-3n + 2≥(1-l) (3
} 的前 n 项和,若对于任意的实数 l∈[0,1], 3Sn-3n + 2≥(1-l) (3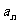 -1) 恒成立,求
n 的取值范围。
-1) 恒成立,求
n 的取值范围。
21.(本小题满分12分) 已知椭圆C的中心为坐标原点O,一个长轴端点为(0,1),短轴端点和焦点所组成的四边形为正方形,若直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且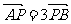 .
.
(Ⅰ)求椭圆C的离心率及其标准方程;
(Ⅱ)求实数m的取值范围.
20.(本小题满分12分) 已知函数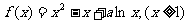 。
。
(Ⅰ)若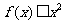 恒成立,求
恒成立,求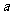 的取值范围;
的取值范围;
(Ⅱ)求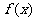 的单调区间.
的单调区间.
19.(本小题满分12分) 在等腰梯形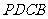 中(如图1),PB=3,DC=1,PD=BC=
中(如图1),PB=3,DC=1,PD=BC=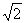 , DA⊥PB于点A;将△PAD沿AD折起,使平面PAD⊥平面ABCD(如图2),点M在棱PB上,平面AMC把几何体P-ABCD分成的两部分体积比
, DA⊥PB于点A;将△PAD沿AD折起,使平面PAD⊥平面ABCD(如图2),点M在棱PB上,平面AMC把几何体P-ABCD分成的两部分体积比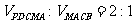
(Ⅰ)确定点M在PB上的位置;
(Ⅱ)判断直线PD是否平行于平面AMC,并说明理由;
(Ⅲ)求二面角M-AC-B的正切值.
18.(本题满分12分) 在一次电视节目的抢答中,题型为判断题,只有“对”和“错”两种结果,其中某选手判断正确的概率为p,判断错误的概率为q,若判断正确则加1分,判断错误则减1分,现记“该选手答完n道题后总得分为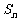 ”。
”。
(Ⅰ)当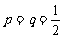 时,记
时,记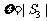 ,求
,求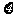 的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)当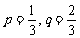 时,求
时,求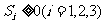 且
且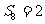 的概率。
的概率。
17.(本题满分12分) 在△ABC中,设A、B、C的对边分别为a、b、c,向量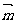 =(cosA,sinA),
=(cosA,sinA),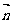 =(
=(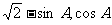 ),若|
),若| |=2.
|=2.
(Ⅰ)求角A的大小;
(Ⅱ)若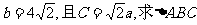 的面积.
的面积.
16.设等边△ABC的边长为a,p是△ABC内任意一点,且P到三边AB、BC、CA的距离分别为 、
、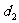 、
、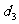 ,则有
,则有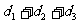 为定值
为定值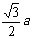 ;由以上平面图形的特性类比到空间图形:设正四面体ABCD的棱长为a,p是正四面体ABCD内任意一点,且P到平面ABC、平面ABD、平面ACD、平面BCD的距离分别为
;由以上平面图形的特性类比到空间图形:设正四面体ABCD的棱长为a,p是正四面体ABCD内任意一点,且P到平面ABC、平面ABD、平面ACD、平面BCD的距离分别为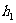 、
、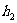 、
、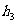 、
、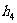 ,则有
,则有
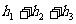 +
+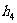 为定值
.
为定值
.
15.在计算机的算法语言中有一种函数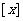 叫做取整函数(也称高斯函数),它表示
叫做取整函数(也称高斯函数),它表示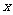 的整数
的整数
部分,即[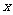 ]是不超过
]是不超过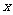 的最大整数.例如:
的最大整数.例如: .设函数
.设函数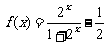 ,则函数
,则函数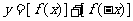 的值域为
.
的值域为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com