21．(本小题满分12分)

　　 设抛物线C₁：的准线与轴交于F₁，抛物线的焦点为F₂，以F₁，F₂为焦点，离心率为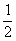的椭圆C₂与抛物线C₁的一个交点为P．

(Ⅰ)当时，直线经过椭圆C₂的右焦点F₂与抛物线C₁交于A₁，A₂两点，如果等于△PF₁F₂的周长，求直线的斜率；

(Ⅱ)求最小实数m，使得△PF₁F₂的各边长均是正整数。

20．(本小题满分12分)

　　 解关于x的不等式．

19．(本小题满分12分)

　　 甲、乙两公司生产同一种产品，但由于设备陈旧，需要更新．经测算，对于函数、　 及任意的≥0，当甲公司投入万元改造设备时，若乙公司投入改造设备费用小于万元，则乙有倒闭的风险，否则无倒闭的风险；同样当乙公司投入万元改造设备时，若甲公司投入改造设备费用小于万元，则甲有倒闭的风险．

(Ⅰ)请解释、g(0)的实际意义．

(Ⅱ)设，，甲、乙公司为了避免恶性竞争，经过协商，同意在双方均无倒闭的风险的情况下尽可能地减少改造设备资金，问此时甲乙两公司各投入多少万元?

18．(本小题满分12分)

　　 如图，已知四棱锥S-ABCD的底面是边长为4的正方形，S在底面上的射影O落在正方　 形内，且O到AB、AD的距离分别为2和1．

(Ⅰ)求证是定值；

(Ⅱ)若P是SC的中点，且SO=3，问在棱SA(不含端点)上是否存在一点Q，使异面直线OP和BQ所成的角为90°?若不存在，说明理由；若存在，求出AQ的长．

17．(本小题满分12分)

　　 已知锐角△ABC，角A，B，C的对边分别为且tanB=

(Ⅰ)求∠B；

(Ⅱ)求sin(B+10°)[1tan(B一10°)]．

16．三个同学对问题“关于的不等式在[1，12]上恒成立，求实数a的取值范围”提出各自的解题思路．

　　 甲说：“只须不等式左边的最小值不小于右边的最大值．”

　　 乙说：“把不等式变形为左边含变量的函数，右边仅含常数，求函数的最值．”

　 　丙说：“把不等式两边看成关于的函数，作出函数图象．”

　　 参考上述解题思路，你认为他们所讨论问题的正确结论，即a的取值范围　　　　　 ．

15．已知，则　　　　　　　 ．

14．抛物线C的顶点在坐标原点，对称轴为y轴，若过点M(0，1)任作一直线交抛物线C于A()、B()两点，且，则抛物线C的方程为　　　　　　　 　　　．

13．观察下式：1=1²，2+3+4=3²，3+4+5+6+7=5²，4+5+6+7+8+9+10=7²，……则可得到一般结论　　　　　　　　　　　　　　　　　　　　　　　　　　　 ．

12．已知，且对任意m,n∈N^*都有①②，则的值为(　　 )

A．　 B．　 C．　 D．

第Ⅱ卷　 (非选择题　 共90分)