3．(坐标系与参数方程)已知曲线C的极坐标方程是．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是：，求直线l与曲线C相交所成的弦的弦长．

2．(矩阵与变换)已知二阶矩阵A的属于特征值－1的一个特征向量为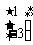，属于特征值3的一个特征向量为，求矩阵A．

1．(几何证明选讲)已知：如图，⊙O与⊙P相交于A，B两点，点P在⊙O上，⊙O的弦BC切⊙P于点B，CP及其延长线交⊙P于D，E两点，过点E作EF⊥CE交CB延长线于点F．若CD=2，CB=2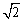，求EF的长．

20．(本小题满分16分)

一个数列中的数均为奇数时，称之为“奇数数列”． 我们给定以下法则来构造一个奇数数列{a_n}，对于任意正整数n，当n为奇数时，a_n=n；当n为偶数时，a_n=．

(1)试写出该数列的前6 项；

(2)研究发现，该数列中的每一个奇数都会重复出现，那么第10个5是该数列的第几项？

(3)求该数列的前2ⁿ项的和T_n．

第Ⅱ卷(附加题 共40分)

19．(本小题满分16分)

已知F₁(－c,0), F₂(c,0) (c＞0)是椭圆的两个焦点，O为坐标原点，圆M的方程是．

(1)若P是圆M上的任意一点，求证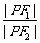：是定值；

(2)若椭圆经过圆上一点Q，且cos∠F₁QF₂=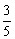，求椭圆的离心率；

(3)在(2)的条件下，若|OQ|=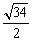，求椭圆的方程．

18．(本小题满分15分)

已知函数f(x)=x²－x+alnx

　　 (1)当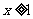时，恒成立，求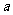的取值范围；

　　 (2)讨论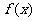在定义域上的单调性；　　　

17．(本小题满分15分)

如图，在长方体ABCD-A₁B₁C₁D₁中，AB= AD=2．

(1)证明：面BDD₁ B₁⊥面ACD₁；

(2)若E是BC₁的中点，P是AC的中点，F是A₁C₁上的点， C₁F=mFA₁，试求m的值，使得EF∥D₁P．

16．(本小题满分14分)

先后2次抛掷一枚骰子，将得到的点数分别记为a,b．

(1)求直线ax+by+5=0与圆x²+y²=1相切的概率；

(2)将a,b,5的值分别作为三条线段的长，求这三条线段能围成等腰三角形的概率．

15．(本小题满分14分)

已知向量=(1+tanx，1－tanx)，=(sin(x－)，sin(x+))．

(1)求证：⊥；

(2)若x∈[－，]，求||的取值范围．

22．(本题满分18分)本题共有3小题，第1小题满分4分，第2小题满分6分，第3小题满分8分。

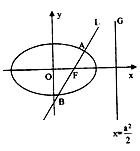
　　　　 如图，已知直线L：的右焦点F，且交椭圆C于A、B两点，直线

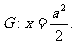
　 (1)求椭圆C的方程；

　 (2)求证：椭圆C上任意一点P到焦点F的距离与到直线G的距离之比为常数，并求出此常数；

　 (3)若直线L交y轴于点M，且当m变化时，求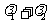的值；