
21.(本小题满分12分)
如图,双曲线C与椭圆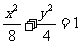 有相同的焦点,直线
有相同的焦点,直线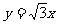 为C的一条渐近线.
为C的一条渐近线.
(1)求双曲线C的方程;
(2)过点P(0,4)的直线l交双曲线C于A、B两点,交x轴于Q点(Q点与双曲线C的顶点不重合). 当 ,求Q点的坐标.
,求Q点的坐标.
20.(本小题满分12分)
(理科)已知数列{an}的前n项和为Sn,对任何正整数n,点Pn(n,Sn)都在函数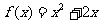 的图象上,且过点Pn(n,Sn)的切线的斜率为Kn.
的图象上,且过点Pn(n,Sn)的切线的斜率为Kn.
(1)求数列{an}的通项公式;
(2)若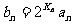 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
(文科)已知函数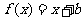 的图象与函数
的图象与函数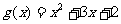 的图象相切,记
的图象相切,记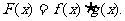
(1)求实数b的值及函数 的极值;
的极值;
(2)若关于x的方程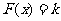 恰有三个不等的实数根,求实数k的取值范围.
恰有三个不等的实数根,求实数k的取值范围.
19.(本小题满分12分)
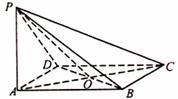
如图,四边形ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
(1)求证:平面PBD⊥平面PAC;
(2)求点A到平面PBD的距离;
(3)求二面角A-PB-D的大小.
18.(本小题满分12分)
袋中有黑球和白球共6个,从中任意取2个球,都是白球的概率为0.4. 现有甲、乙两人从袋中轮流摸取一个球,甲先取乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止时所需要的取球次数.
(1)求袋中原有白球的个数;
(2)(理科)求随机变量ξ的概率分布及期望,并求甲取到白球的概率.
(文科)求乙取到白球的概率.
17.(本小题满分12分)
在△ABC中,a、b、c分别为角A、B、C的对边,且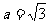 ,b+c=3,当边b和c为何值时,
,b+c=3,当边b和c为何值时, 取得最大值.
取得最大值.
16.(理科)设O为坐标原点,点M(2,1),若点N(x,y)满足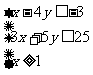 ,则
,则
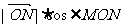 的最大值为
的最大值为
|
 的最小值为
的最小值为
15.有6个座位连成一排,安排3人就座,恰有两个空位相邻的不同坐法有 种
14.已知数列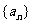 满足
满足
13.正四棱锥S-ABCD的底面边长和各侧棱长都为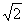 ,点S、A、B、C、D都在同一个球面上,则该球的体积为
.
,点S、A、B、C、D都在同一个球面上,则该球的体积为
.
12.在正三角形ABC中,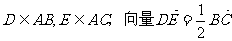 ,则以B、C为焦点,且过D、E的双曲线的离心率为 ( )
,则以B、C为焦点,且过D、E的双曲线的离心率为 ( )
A.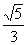 B.
B.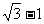 C.
C.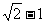 D.
D.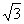 +1
+1
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com