5．若三个平面两两相交，则它们的交线的条数是

(A)1　　 　　　　　　　　 (B)2　　 　　　　　　　　 (C)3　　　　　　　　　　　　 (D)1，或3

4．下图为一个几何体的三视图，则这个几何体是

(A)由一个四棱柱和一个棱锥组合而成的简单几何体

(B)由一个四棱柱和一个圆锥组合而成的简单组合体

(C)由一个圆柱和一个圆锥组合而成的简单几何体

(D)由一个正方体和一个圆锥组合而成的简单几何体

3．函数的定义域是

(A)[4，+∞)　　 　　　　　　　　　　　　　　　　　　　 (B)(10，+∞)

(C)(4，10)∪(10，+∞)　 　　　　　　　　　 (D)[4，10)∪(10，+∞)

2．函数的图象为

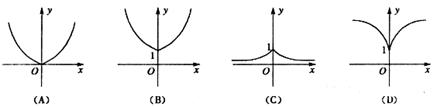
1．设全集U={0，－1，－2，－3，－4}，集合M={0，－1，－2}，N={0，－3，－4}，那么(M)∩N等于

(A){0}　　 　　　　　　　 (B){－3，－4)　　　 (C){－1，－2}　　　　 (D)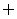

22．(本题满分18分)本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分.

设抛物线的焦点为，经过点的直线交抛物线于、两点，且、两点坐标分别为，是抛物线的准线上的一点，是坐标原点．若直线、、的斜率分别记为：、、，(如图)

　 (1)若，求抛物线的方程．

　 (2)当时，求的值．

　 (3)如果取， 时，

(文科考生做)判定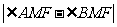和的值大小关系．并说明理由．

　 (理科考生做)判定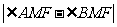和的值大小关系．并说明理由．

通过你对以上问题的研究，请概括出在怎样的更一般的条件下，使得你研究的结果(即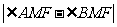和的值大小关系)不变，并证明你的结论．

21．(本题满分16分)本题共有3个小题，第1小题满3分，第2小题满分5分，第3小题满分8分.

在等差数列中，公差，且，

(1)求的值．

　 (2)当时，在数列中是否存在一项(正整数)，使得 　， ，成等比数列，若存在，求的值；若不存在，说明理由．

(3)若自然数(为正整数)

满足< << 　< <， 使得成等比数列，

　 (文科考生做)当时，　 用表示 ．　

　 (理科考生做)求的所有可能值．

20．(本题满分14分)本题共有2个小题，第1小题满分6分，第2小题满分8分.

上海某玩具厂生产套2008年奥运会吉祥物“福娃”所需成本费用为元，且，而每套售出的价格为元，其中 ，

　 (1)问：该玩具厂生产多少套“福娃”时，使得每套“福娃”所需成本费用最少？

　 (2)若生产出的“福娃”能全部售出，且当产量为150套时利润最大，此时每套价格为30元，求的值．(利润 = 销售收入 - 成本)

19．(本题满分14分)本题共有2个小题，第1小题满分6分，第2小题满分8分.

设函数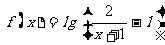的定义域为集合，函数的定义域为集合．

　 (1)(文科考生做)当时，求集合.

(理科考生做)判定函数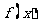的奇偶性，并说明理由.

　 (2)问：是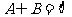的什么条件(充分非必要条件 、必要非充分条件、充要条件、既非充分也非必要条件)？并证明你的结论.

18．(本题满分12分)本题共有2个小题，第1小题满分6分，第2小题满分6分.

已知向量　

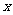　 (1)当时，求的值.

　 (2)(文科考生做)求·的最大值与最小值.

　 (理科考生做)求·， 在上的最大值与最小值.