1．复数i(1一i)等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　 　 A．1+i　　 　　　　　　　 B．1一i　　 　　　　　　 C．一1+i　　 　　　　　 D．一1一i

22．(本题满分14分)椭圆C的中心为坐标原点O，焦点在y轴上，离心率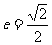，椭圆上的点到焦点的最短距离为与y轴交于P(0，m)，与椭圆C交于相异两点A、B，且

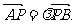
　 (1)求椭圆方程；

　 (2)若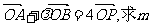的取值范围。

21．(本小题满分12分)设函数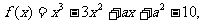若它是R上的单调函数，且1是它的零点。

　 (1)求实数a的值；

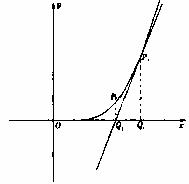
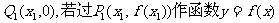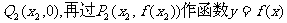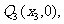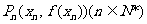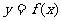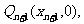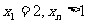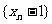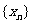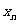　 (2)设的图象的切线与x轴交于点的图象的切线与x轴于……，依此下去，过作函数的图象的切线与x轴交于点……，若求证：成等比数列；并求数列的通项公式。(已知)

20．(本小题满分12分)已知函数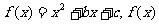满足条件：

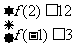……………………①

　 (1)求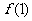的取值范围；

　 (2)若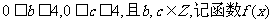满足条件①的事件为A，求事件A发生的概率。

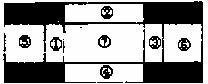
19．(本小题满分12分)将一张2×6米的硬钢板按图纸的要求进行操作：沿线裁去阴影部分，把剩余的部分按要求焊接成一个有盖的长方体水箱(⑦为底，①②③④为侧面，⑤+⑥为水箱盖，其中①与③、②与④分别是全等的矩形，且⑤+⑥=⑦)，设水箱的高为x米，容积为y立方米。

　 (1)写出y关于x的函数关系式；

　 (2)如何设计x的大小，使得水箱的容积最大？

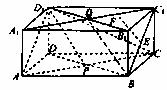
18．(本题满分12分)如图，在长方体ABCD-A₁B₁C₁D₁中，AB=AD=2。

　 (1)证明：面BDD₁B₁⊥面ACD₁；

　 (2)若E是BC₁的中点，P是AC的中点，A₁C₁∩B₁D₁，F是A₁C₁上的点，C₁F=mFA₁，试求m的值，使得EF//D₁P。

17．(本小题满分12分)已知△ABC三个内角A、B、C的对边分别为a、b、c，向量。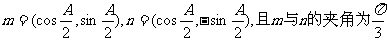

　 (1)求A；

　 (2)已知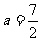，求bc的最大值。

16．已知函数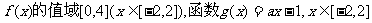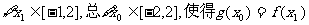，成立，则实数a的取值范围是　　　　　 。

15．两个正数m,n的等差中项是5，等比中项是4。若m>n，则椭圆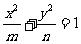的离心率e的大小为　　　　　 。

14． 若一个圆的圆心在抛物线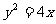的焦点上，且此圆与直线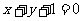相切，则这个圆的方程是　　　　　 。