
11.已知A,B,C是△ABC的三个内角,则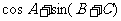 的最大值为
。
的最大值为
。
21.(本小题满分13分)
设抛物线C: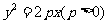 过点
过点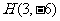 ,其准线为
,其准线为 ,焦点为F。
,焦点为F。
(1)求抛物线C的方程;
(2)若准线 与
与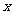 轴的交点为M,AB是经过焦点F的抛物线的任意弦,记
轴的交点为M,AB是经过焦点F的抛物线的任意弦,记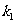 为MA的斜率,
为MA的斜率,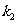 为MB的斜率,求
为MB的斜率,求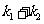 的值;
的值;
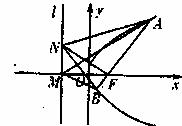
(3)试探究:对于抛物线的准线 上的任意一点N,经过焦点F的抛物线的任意弦AB,记
上的任意一点N,经过焦点F的抛物线的任意弦AB,记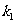 为NA的斜率,
为NA的斜率,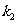 为NB的斜率,
为NB的斜率, 为NF的斜率,是否有
为NF的斜率,是否有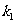 、
、 、
、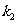 成等差数列,请说明理由。
成等差数列,请说明理由。
20.(本小题满分13分)
设函数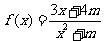 的图象过点A(2,2),
的图象过点A(2,2),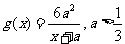
(1)求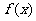 的解析式;
的解析式;
(2)求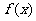 的极大值与极小值;
的极大值与极小值;
(3)若对任意的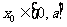 ,总存在相应的
,总存在相应的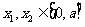 ,使得
,使得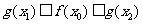 成立,试求实数
成立,试求实数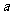 的取值范围。
的取值范围。
19.(本小题满分13分)
在数列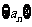 中,前
中,前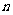 项和为
项和为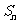 。已知
。已知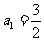 ,
, 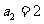 且
且

(1)求数列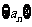 的通项公式;
的通项公式;
(2)设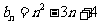 ,试求最小的正整数
,试求最小的正整数 ,使得对一切正整数
,使得对一切正整数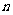 ,均有
,均有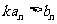 。
。
18.(本小题满分12分)
某大型体育网站对2008年北京奥运会部分体育竞技项目进行预测,其中进入女子羽毛球团体决赛的队伍可能是中国女羽与印尼女羽,由于奥运会女羽冠军争夺是以“五局三胜”制进行,根据以往战况,中国女羽每一局赢的概率为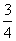 ,倘若在比赛中,第一局印尼女羽先胜一局,在这个条件下:
,倘若在比赛中,第一局印尼女羽先胜一局,在这个条件下:
(1)求中国女羽取胜的概率(用分数作答);
(2)设决赛中比赛总的局数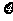 ,求
,求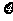 的分布列及
的分布列及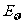 (用分数作答)。
(用分数作答)。
17.(本小题满分12分)
如图所示,直三棱柱ABC-A1B1C1中,AC=BC=1,∠ACB=90°,点D为AB的中点。

(1)求证:BC1 ∥面A1DC;
(2)求棱AA1的长,使得A1C与面ABC1所成角的正弦值等于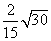 。
。
16.(本题满分12分)
已知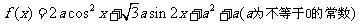
(1)若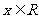 ,求
,求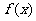 的最小正周期;
的最小正周期;
(2)若对任意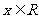 时,
时,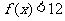 恒成立,求
恒成立,求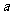 的取值范围。
的取值范围。
15.对于函数 ,给出下列命题:①当
,给出下列命题:①当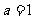 时,
时,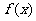 在定义域上为单调增函数;②
在定义域上为单调增函数;②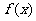 的图象的对称中心为
的图象的对称中心为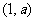 ;③对任意
;③对任意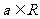 ,
,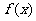 都不是奇函数;④当
都不是奇函数;④当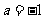 时,
时,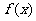 为偶函数;⑤当
为偶函数;⑤当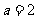 时,对于满足条件
时,对于满足条件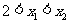 的所有
的所有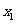 ,
,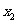 总有
总有 。其中正确命题的序号为
。
。其中正确命题的序号为
。
14.在直角坐标系中,点P到点F(2,0)的距离为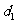 ,点P到
,点P到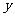 轴的距离为
轴的距离为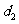 ,若
,若
 ,则点
,则点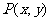 的轨迹方程为
。
的轨迹方程为
。
13.若曲线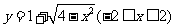 与直线
与直线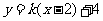 有两个交点,则实数
有两个交点,则实数 的取值范围是
。
的取值范围是
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com