
20.(本小题满分12分)
已知数列{an}和等比数列{bn}满足a1=b1=4,a2=b2=2,a3=1,且数列{an+1-an}是等差数列,n∈N*.
(I)求数列{an}和{bn}的通项公式;
(II)是否存在k∈N*,使得ak-bk∈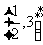 ?若存在,求出k的值;若不存在,请说
?若存在,求出k的值;若不存在,请说
明理由.
19.(本小题满分12分)
(新华网)反兴奋剂的大敌、服药者的宠儿--HGH(人体生长激素),有望在8月的北京奥运会上首次“伏法”.据悉,国际体育界研究近10年仍不见显著成效的HGH检测,日前已取得新的进展,新生产的检测设备有希望在北京奥运会上使用.
若组委会计划对参加某项田径比赛的120名运动员的血样进行突击检查,采用如下化验方法:将所有待检运动员分成若干小组,每组m个人,再把每个人的血样分成两份,化验时将每个小组内的m个人的血样各一份混合在一起进行化验,若结果中不含HGH成分,那么该组的m个人只需化验这一次就算检验合格;如果结果中含有HGH成分,那么需要对该组进行再次检验,即需要把这m个人的另一份血样逐个进行化验,才能最终确定是否检验合格,这时,对这m个人一共需要进行m+1次化验.假定对所有人来说,化验结果中含有HGH成分的概率均为.当m=3时,
(I)求一个小组只需经过一次检验就合格的概率;
(II)设一个小组的检验次数为随机变量ξ,求ξ的分布列及数学期望.
18.(本小题满分12分)
如图,斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥侧面ABB1A1,AC=AB=,
∠CAA1=∠BAA1=135°.
(I)求∠BAC的大小;
(II)若底面△ABC的重心为G,侧棱AA1=4,求GC1与平面A1B1C1所成角的大小.


17.(本小题满分12分)
已知函数f(x)=sinωxcosωx-cos2ωx+(ω>0,x∈R)的最小正周期为.
(I)求f()的值,并写出函数f(x)的图象的对称中心的坐标;
(II)当x∈[,]时,求函数f(x)的单调递减区间.
16.设定义域为[x1,x2]的函数y=f(x)的图象为C,图象的两个端点分别为A、B,点O为坐标原点,点M是C上任意一点,向量=(x1,y1),=(x2,y2),=(x,y),满足x=λx1+(1-λ)x2(0<λ<1),又有向量=λ+(1-λ),现定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指||≤k恒成立,其中k>0,k为常数。
根据上面的表述,给出下列结论:①A、B、N三点共线;②直线MN的方向向量可以为=(0,1);③“函数y=5x2在[0,1]上可在标准1下线性近似”;④“函数y=5x2在[0,1]上可在标准下线性近似”.其中所有正确结论的番号为_______________.
15.连续抛掷一枚骰子两次,得到的点数依次记为m、n,则点(m,n)恰能落在不等式组所表示的区域内的概率为_______________.
14.设关于x的方程x2+ax-2=0的两根为x1、x2,当x1<1<x2时,实数a的取值范围是
_________________.
13.求和:1-C1013+C10232-C10333+……+C1010310=______________.
12.已知全集U,集合A、B为U的非空真子集,若“x∈A”与“x∈B”是一对互斥事件,则称A与B为一组U(A,B)。规定:U(A,B)≠U(B,A)。当集合U={l,2,3,4,5}时,所有的U(A,B)的组数是 ( )
A.70 B.30 C.180 D.150
|
11.已知P是椭圆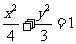 上的一点,F1、F2是该椭圆的两个焦点,若△PF1F2的内切圆半径为
上的一点,F1、F2是该椭圆的两个焦点,若△PF1F2的内切圆半径为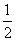 ,则
,则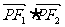 的值为 ( )
的值为 ( )
A.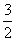 B.
B.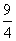 C.
C.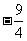 D.0
D.0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com