18．(本小题满分12分)

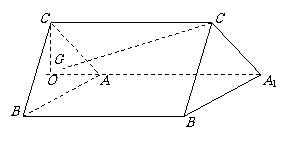
如图，斜三棱柱ABC－A₁B₁C₁中，顶点C在侧面ABB₁A₁内的射影O恰好在AA₁的延长线上，AC＝AB＝，∠CAA₁＝∠BAA₁＝135°.

　 (1)求∠BAC的大小；

　 (2)若底面△ABC的重心为G，侧棱AA₁＝4，求GC₁与平面A₁B₁C₁所成角的大小.

17．(本小题满分12分) 已知函数f(x)＝sinωxcosωx－cos²ωx+(ω＞0，x∈R)的最小正周期为.

　 (1)求f()的值，并写出函数f(x)的图象的对称中心的坐标；

　 (2)当x∈[，]时，求函数f(x)的单调递减区间.

16．已知函数f(x)＝log_a(+bx)(a＞0且a≠1)，给出如下判断：①函数f(x)为R上的偶函数的充要条件是b＝0；②若a＝，b＝－1，则函数f(x)为R上的减函数；③当a＞1时，函数f(x)为R上的增函数；④若函数f(x)为R上的奇函数，且为R上的增函数，则必有0＜a＜1，b＝－1或a＞1，b＝1.其中所有正确结论的番号为_______________.

15．已知变量x．y满足约束条件，则目标函数z＝的最小值为_______________.

14．求和：1－C₁₀¹3+C₁₀²3²－C₁₀³3³+……+C₁₀¹⁰3¹⁰＝______________.

13．等差数列{a_n}(n∈N^*)中，a₃+a₁₃－2a₇＝－2，则此数列的公差d＝_______________.

12．已知P是椭圆＝1上一点，F₁．F₂是该椭圆的两个焦点，若△PF₁F₂的内切圆半径为，则的值为　 (　　 )

　　　 A．　　　　　　　　　　　　 B．－　　　　　　　　　　 C．　　　　　　　　　　　　 D．0

第二卷(非选择题，共计90分)

11．如图，若底面边长为2的正四掕锥P－ABCD的斜高为，

则此正四掕锥外接球的体积为　　　　　　　　 (　　 )

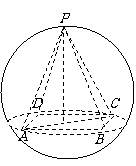
　A．9π　　　　　　　　　　 B． C．3π　　　　　　　　　　　 D．12π

10．2008北京奥运会的第一批志愿者将在7月初正式上岗.现随机安排该批志愿者到三个比赛场地服务，则其中来自四川的3名志愿者恰好被安排在两个不同场地服务的概率是

　　　 A．　　　　　　　　　　　　 B．　　　　　　　　　　　　 C．　　　　　　　　　　　 D．

9．在△ABC中，若·＝1，·＝－2，则||的值为　　　　　　　　　　　　　　　 (　　 )

　　　 A．1　　　　　　　　　　　　 B．3　　　　　　　　　　　　 C．　　　　　　　　　　 D．