
2.下列各选项中,与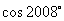 最接近的数是 ( )
最接近的数是 ( )
A. 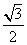 B.
B.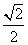 C.
C.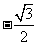 D.
D. 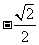
1.已知集合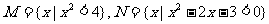 ,则集合
,则集合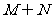 = ( )A.{
= ( )A.{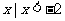 } B.{
} B.{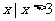 } C.{
} C.{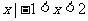 } D.{
} D.{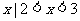 }
}
21.(14分)椭圆G: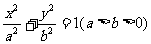 的两个焦点为F1、F2,短轴两端点B1、B2,已知F1、F2、B1、B2四点共圆,且点N(0,3)到椭圆上的点最远距离为
的两个焦点为F1、F2,短轴两端点B1、B2,已知F1、F2、B1、B2四点共圆,且点N(0,3)到椭圆上的点最远距离为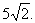
(1)求此时椭圆G的方程;
(2)设斜率为k(k≠0)的直线m与椭圆G相交于不同的两点E、F,Q为EF的中点,问E、F两点能否关于过点P(0,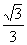 )、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
)、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
20.(14分)已知数列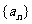 的前n项和为
的前n项和为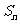 ,且满足
,且满足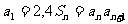
(1)求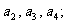
(2)求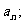
(3)若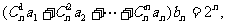 求证:
求证: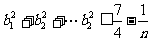 .
.
19.(14分)已知函数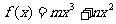 (m、n∈R,m≠0)的图像在(2,
(m、n∈R,m≠0)的图像在(2, )处的切线与x轴平行.
)处的切线与x轴平行.
(1)求n,m的关系式并求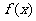 的单调减区间;
的单调减区间;
(2)证明:对任意实数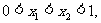 关于x的方程:
关于x的方程:
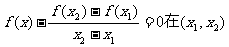 恒有实数解.
恒有实数解.
(3)结合(2)的结论,其实我们有拉格朗日中值定理:若函数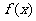 是在闭区间[a,b]上连续不断的函数,且在区间(a,b)内导数都存在,则在(a,b)内至少存在一点x0,使得
是在闭区间[a,b]上连续不断的函数,且在区间(a,b)内导数都存在,则在(a,b)内至少存在一点x0,使得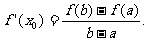 如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
当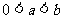 时,
时,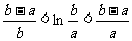 (可不用证明函数的连续性和可导性)
(可不用证明函数的连续性和可导性)
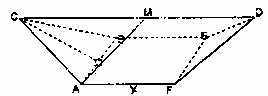
18.(14分)如图,已知几何体ABC-DEF中,△ABC及△DEF都是边长为2的等边三角形,四边形ABEF为矩形,且CD=AF+2,CD∥AF,O为AB中点.
(1)求证:AB⊥平面DCO.
(2)若M为CD中点,AF=x,则当x取何值时,使AM与平面ABEF所成角为45°?试求相应的x值.
(3)求该几何体在(2)的条件下的体积.
17.(12分)某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试.假设某学生每次通过测试的概率都是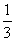 ,每次测试时间间隔恰当,每次测试通过与否互相独立.
,每次测试时间间隔恰当,每次测试通过与否互相独立.
(1)求该学生考上大学的概率.
(2)如果考上大学或参加完5次测试就结束,记该生参加测试的次数为ξ,求ξ的分布列及ξ的数学期望.
16.(12分)已知:函数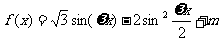 的周期为
的周期为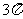 ,且当
,且当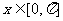 时,函数
时,函数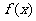 的最小值为0.
的最小值为0.
(1)求函数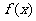 的表达式;
的表达式;
(2)在△ABC中,若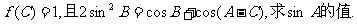
12.有一地球同步卫星A与地面四个科研机构B、C、D、E,它们两两之间可以相互接发信息,由于功率有限,卫星及每个科研机构都不能同时向两处发送信息(例如A不能同时给B、C发信息,它可先发给B,再发给C),它们彼此之间一次接发信息的所需时间如右图所示.则一个信息由卫星发出到四个科研机构都接到该信息时所需的最短时间为________.
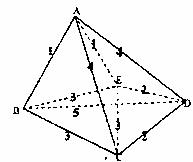
13(选做题).在极坐标系中,以ρcOsθ+1=0为准线,(1,0)为焦点的抛物线的极坐标方程为_______________.
14(选做题).不等式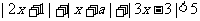 的解集非空,则
的解集非空,则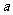 的取值范围为___________.
的取值范围为___________.
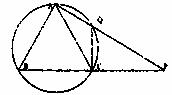
15(选做题).在圆内接△ABC中,AB=AC=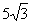 ,Q为圆上一点,AQ和BC的延长线交于点P(如图),且AQ:QP=1:2,则AP=_________.
,Q为圆上一点,AQ和BC的延长线交于点P(如图),且AQ:QP=1:2,则AP=_________.
11.观察:①tan10°·tan20°+tan20°·tan60°+tan60°·tan10°=1;
②tan15°·tan25°+tan25°·tan50°+tan50°·tan15°=1;
③tan13°·tan27°+tan27°·tan50°+tan50°·tan13°=1.已知以上三式成立且还有不少类似的等式成立,请你再写出一个这样的式子:______________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com