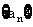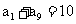1．在等差数列中，，则前9项和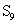，等于A．

A．10　　 　　　　　　　　　 B．45　　 　　　　　　　　　 C．90　　 　　　　　　　　　 D．100

22．(本小题满分14分)

椭圆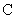的一个焦点坐标为(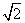，0)，过此焦点且垂直于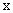轴的弦的长等于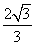

(I)求椭圆C的方程；

(Ⅱ)设直线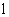与椭圆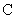交于A，B两点，坐标原点O到直线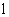的距离为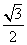，求△OAB面积的最大值。

21．(本小题满分12分)

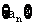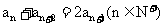数列满足，且。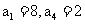

(I)求数列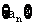的通项公式；

(Ⅱ)设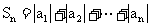，求；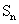

(Ⅲ)设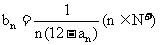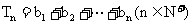，，是否存在最大整数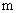，使得对任意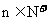，均有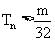成立？若存在，求出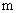的值；若不存在，说明理由。

20．(本小题满分12分)

某工厂经过技术改造和设备更新后，预计第一年的年产量的增长率为100%，从第二年起，以后每年的增长率都是前一年增长率的一半；生产过程中，估计每年将损失年产量的2%(损失的部分不计人年产量)，设技术更新前每年的年产量是a。

(I)写出技术改造后的第一年，第二年的年产量，并写出第n年与第n－1年(n≥2， n∈N)的年产量之间的关系式；

(Ⅱ)请说明从第几年起年产量将比上一年减少。

19．(本小题满分l2分)

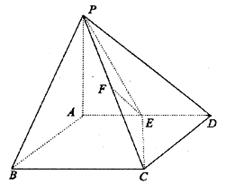
如图，在四棱锥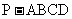中，PA⊥平面ABCD，底面 ABCD为正方形，且PA＝AD＝2，E是AD的中点，F是PC上的点。

(I)若EF∥平面PAB，试确定F点位置；

(Ⅱ)求二面角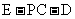的大小。

18．(本小题满分12分)

设点P(x，y)为平面直角坐标系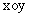中的一个动点(O为坐标原点)，点P到定点A(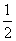，0)的距离比点P到y轴的距离大。

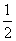(I)求点P的轨迹C的方程；

(Ⅱ)若点M是C上任意一点，过M作x轴的垂线段MN，N为垂足，求线段MN的中点H的轨迹。

17．(本小题满分12分)

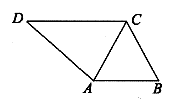
如图，四边形ABCD中，DC∥AB，设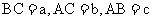，且。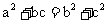

(I)求∠CAB的大小；

(Ⅱ)若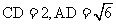，求△ACD的面积S。

16．在平面直角坐标系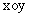中，已知△ABC的顶点A(一4，0)和C(4，0)，顶点B在椭圆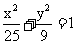，则　　　　　　　 。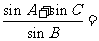

15．在R上定义运算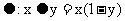，若不等式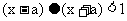对任意的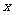都成立，则实数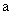的取值范围是　　 　　　　　　　 。

14．正方体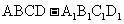中，E，F分别为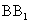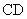，的中点，则直线EF与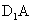所成角的余弦值 　　　　　　　　　 。