
5.设m、n是两条不同直线, 是三个不同的平面,给出如下四个命题:
是三个不同的平面,给出如下四个命题:
① ②
②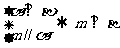
③ ④
④
其中假命题是 ( )
A.①、② B.②、③ C.①、③ D.②、④
3.过点 的直线l经过圆
的直线l经过圆 的圆心,则直线l的倾斜角为 ( )
的圆心,则直线l的倾斜角为 ( )
A.120° B.150° C.60° D.30°
2.若i为虚数单位,则 等于 ( )
等于 ( )
A. B.
B. C.
C. D.-
D.-
1.在下列各数中,与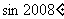 的值最接近的是 ( )
的值最接近的是 ( )
A. B.
B. C.-
C.- D.-
D.-
22.(本小题共14分)
椭圆C: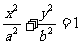 (
( >b>0)的两个焦点为F1,F2,点P在椭圆C上,且PF1⊥F1F2,
>b>0)的两个焦点为F1,F2,点P在椭圆C上,且PF1⊥F1F2, =
= ,
, .
.
(1)求椭圆C的方程;
(2)若直线 过圆
过圆 的圆心M,交椭圆C于A,B两点,且A,B关于点M对称,求直线
的圆心M,交椭圆C于A,B两点,且A,B关于点M对称,求直线 的方程.
的方程.
21.(本小题共12分)
已知函数 (
( ,b为常数),其导函数
,b为常数),其导函数 的图象过点(2,一1).
的图象过点(2,一1).
(1)求 的单调区间及极值;
的单调区间及极值;
(2)若b=15-4ln3,确定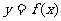 的图像与
的图像与 轴交点的个数.
轴交点的个数.
20.(本题满分12分)
已知定点A(0,1),B(0,-1)动点P满足 .
.
(1)求动点P的轨迹方程,并说明方程表示的曲线;
(2)当k=2时求曲线上点与点(2,0)距离的最大值和最小值。
19.(本小题满分12分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.

(1)请根据上表提供的数据,用最小二乘法求出y关于 的线性回归方程
的线性回归方程 =
= +
+ .
.
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
18.(本题满分12分)
已知p:函数= 与
与 轴有两个不同交点,q:方程
轴有两个不同交点,q:方程 =(
=( 2一
2一 )
) 表示开口向右的抛物线.若“p
表示开口向右的抛物线.若“p q”为真命题,“p
q”为真命题,“p q”为假命题,求实数
q”为假命题,求实数 的范围.
的范围.
17.(本题满分12分)
画出“输入正整数n后,计算S=n×(n一1) ×…×3×2×1”的程序框图。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com