
3.如图表示甲、乙两名篮球运动员每场比赛得分情况的茎叶图,则甲和乙得分的中位数的和是 ( )

A.56分 B.57分 C.58分 D.59分
2.若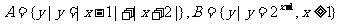 ,则(
,则(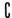 RA)∩B为( )
RA)∩B为( )
A.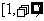 B.
B.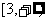 C.(0,3) D.
C.(0,3) D.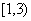
1.设复数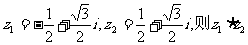 = ( )
= ( )
A.1 B.i C.-1 D.-i
22.已知函数
(1)讨论函数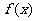 的单调性;
的单调性;
(2)k是偶数时,正项数列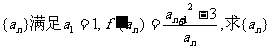 的通项公式;
的通项公式;
(3)k是奇数,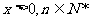 时,求证:
时,求证:
21.如图,已知点F(2,0),直线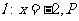 为该平面上的动点,过P做直线l的垂直,垂足为Q,且
为该平面上的动点,过P做直线l的垂直,垂足为Q,且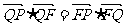

(1)求动点P的轨迹C的方程;
(2)设过A(-2,0)的直线m交轨迹C于M,N两点,且∠MFN为锐角,求直线m的斜率k的取值范围.
20.设函数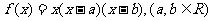 .
.
(1)若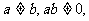 过两点(0,0)、(a,0)的中点作与x轴垂直的直线,此直线与函数
过两点(0,0)、(a,0)的中点作与x轴垂直的直线,此直线与函数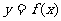 的图象交于点
的图象交于点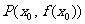 ,求证函数
,求证函数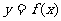 的点p处的切点过点(b,0);
的点p处的切点过点(b,0);
(2)若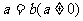 ,且当
,且当 时
时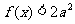 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
19.如图,已知四棱锥P-ABCD的底面ABCD为等腰三角梯形,AB∥CD,AC⊥BC,AC∩BD=0,且顶点P在底面上的射影恰为O点,又OB=2,OP=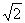 ,PD⊥PD.
,PD⊥PD.
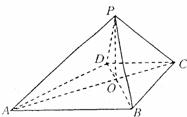
(1)求二面角B-PA-D的余弦的绝对值;
(2)在棱PC上是否存在点M,使PC⊥平面BMD?若存在,求出点M的位置;若不存在,试说明理由。
(3)在(2)的条件下,求三棱锥C-BMD的体积.
18.2008年中国北京奥运会吉祥物由5个“中国福娃”组成,分别叫贝贝、晶晶、欢欢、迎迎、妮妮。现有8个相同的盒子,每个盒子中放一只福娃,每种福娃的数量如下表:
|
福娃名称 |
贝贝 |
晶晶 |
欢欢 |
迎迎 |
妮妮 |
|
数量 |
1 |
2 |
3 |
1 |
1 |
从中随机地选取5只。
(1)求选取的5只恰好组成完整“奥运吉祥物”的概率;
(2)若完整地选取奥运会吉祥物记100分;若选出的5只中仅差一种记80分;差两种记60分;以此类推。设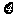 表示所得的分数,求
表示所得的分数,求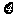 的分布列和期望值。
的分布列和期望值。
17.在△ABC中,边a,b,c的对角分别为A、B、C,且
(1)求角B的值;
(2)求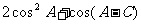 的范围。
的范围。
16.定义在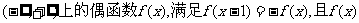 在[0,1]上是减函数。下面四个关于
在[0,1]上是减函数。下面四个关于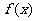 的命题
的命题
①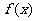 是周期函数;②
是周期函数;②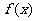 的图象关于x=1对称;③
的图象关于x=1对称;③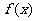 在[-1,0]上是减函数;
在[-1,0]上是减函数;
④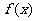 在[1,2]上为增函数。其中真命题的序号为
.
在[1,2]上为增函数。其中真命题的序号为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com