
7.一个几何体的三视图如图所示,其中正视图和侧视图是腰长为6的两个等腰直角三角形,该几何体的体积为

A.54 B.72
C.108 D.216
6.已知 ,则
,则 的值为
的值为
A.4 B.3
C.-4 D.-3
5.如图为正方体 ,沿棱由A到
,沿棱由A到 点按最短的路线行进,在所有的路线中,按照A→B→
点按最短的路线行进,在所有的路线中,按照A→B→ →
→ 路径行进的概率为
路径行进的概率为

A. B.
B.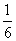 C.
C.  D.
D.
4.将指数函数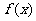 的图像向右平移一个单位,得到如图所示的
的图像向右平移一个单位,得到如图所示的 的图像,则
的图像,则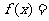

A.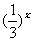 B.
B.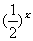
C. D.
D.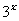
3.过点( ,-2)的直线
,-2)的直线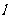 经过圆:
经过圆: 的圆心,则直线
的圆心,则直线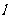 的倾斜角的大小为
的倾斜角的大小为
A. B.
B. C.
C. D.
D.
2.已知函数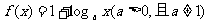 的图像过点(4,3),则
的图像过点(4,3),则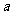 等于
等于
A. B.
B. C.
C. D.
D.
1.已知全集I={-1,-2,-3,0,1},M={-1,0,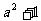 },则
},则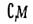 为
为
A.{-1,0,1} B.{-2,-3} A.
C.{-1,-3} D.{-1,-2,-3,1}
(17)(本小题满分12分)
在△ABC中,已知内角 ,边
,边 ,设内角
,设内角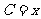 ,周长为
,周长为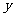 。
。
(Ⅰ)求函数 的解析式和定义域;
的解析式和定义域;
(Ⅱ)求函数 的最大值及单调递增区间。
的最大值及单调递增区间。
(18)(本小题满分12分)
如图,已知直四棱柱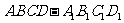 中底面ABCD为平行四边形。
中底面ABCD为平行四边形。 ,AD=BD,E是
,AD=BD,E是 的中点,
的中点,
(Ⅰ)求证: 平面BDE;
平面BDE;
(Ⅱ)求二面角B-DE-C的余弦值。

(19)(本小题满分12分)
某养殖厂需定期购买饲料,已知该厂每天需要饲料200公斤,每公斤饲料的价格为1.8元,饲料的保管与其他费用为平均每公斤每天0.03元,购买饲料每次支付运费300元。(注:每隔 天购买一次,保管的天数为
天购买一次,保管的天数为 。)
。)
(Ⅰ)求该厂多少天购买一次饲料才能使平均每天支付的总费用最小;
(Ⅱ)若提供饲料的公司规定,当一次购买饲料不少于5吨时其价格可享受八五折优惠(即原价的85%)。问该厂是否考虑利用此优惠条件,请说明理由。
(20)(本小题满分12分)
已知函数 在区间[-1,1]上是增函数。
在区间[-1,1]上是增函数。
(Ⅰ)求实数a的值所组成的集合A;
(Ⅱ)设关于 的方程
的方程 的两实数根为
的两实数根为 ,
,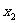 ,试问:是否存在实数
,试问:是否存在实数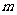 ,使得不等式
,使得不等式 对任意
对任意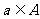 及
及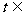 [-1,1]恒成立?若存在,求出
[-1,1]恒成立?若存在,求出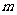 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
(21)(本小题满分12分)
如图,设 ,
,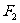 是椭圆C:
是椭圆C: 焦点,A,B分别是椭圆C的上顶点和右顶点,P是椭圆C上在一象限内的一点,O为坐标原点,已知
焦点,A,B分别是椭圆C的上顶点和右顶点,P是椭圆C上在一象限内的一点,O为坐标原点,已知 ,
, 。
。
(Ⅰ)设椭圆C的离心率为 ,证明:
,证明: ;
;
(Ⅱ)证明: ;
;
(Ⅲ)设 ,求椭圆的长轴长。
,求椭圆的长轴长。

(22)(本小题满分14分)
已知函数 是定义在
是定义在 上的函数,且满足
上的函数,且满足 ,
, ,设
,设 ,
, ,
,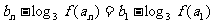 。
。
(Ⅰ)求证: ;
;
(Ⅱ)若 对任意的
对任意的 恒成立,求
恒成立,求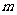 的取值范围。
的取值范围。
(13)不等式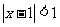 的解集是 。
的解集是 。
(14)已知双曲线 的一条渐近线方程为
的一条渐近线方程为 ,则双曲线的离心率为 。
,则双曲线的离心率为 。
(15)正四棱锥P-ABCD的底面ABCD在球O的大圆面上,顶点P在球面上,已知球的体积为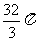 ,则正四棱锥P-ABCD体积的最大值是
,则正四棱锥P-ABCD体积的最大值是
(16)函数 满足
满足 (
(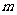 为大于零的常数),且正实数
为大于零的常数),且正实数 ,
,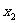 满足
满足 ,则
,则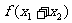 的最小值为 。
的最小值为 。
(1)已知集合 ,
,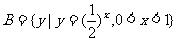 ,则
,则 为
为
A.(0, )
B.(
)
B.( ,
, )
C.(
)
C.( ,1) D.(0,2)
,1) D.(0,2)
(2)直线 与曲线
与曲线 所围成封闭图形的面积是
所围成封闭图形的面积是
A.6 B.9 C.12 D.15
(3)有一个正三棱柱,其三视图如下:则其体积等于

A. B.
B. C.
C.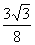 D.
D.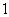
(4)设函数, 若
若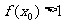 ,则
,则 的取值范围是
的取值范围是
A.(-1,1) B.(-1, )
)
C.( ,-2)
,-2) (0,
(0, )
D.(
)
D.( ,-1)
,-1) (1,
(1, )
)
(5)下列命题错误的是
A.命题“若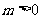 ,则方程
,则方程 有实数根”的逆否命题为:“若方程
有实数根”的逆否命题为:“若方程 无实根,则
无实根,则 ”
”
B.“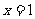 ”是“
”是“ ”的充分不必要条件
”的充分不必要条件
C.若 为假命题,则p、q均为假命题
为假命题,则p、q均为假命题
D.对于命题 ,使得
,使得 ,则
,则 ,均有
,均有
(6)已知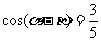 ,
,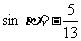 ,且
,且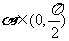 ,
, ,则
,则
A. B.
B.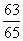 C.
C. D.
D.
(7)各项都是正数的等比数列 的公比
的公比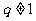 ,且
,且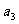 ,
, ,
, 成等差数列,则
成等差数列,则
A. B.
B. C.
C.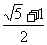 D.
D.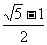
(8)过抛物线 的焦点的直线
的焦点的直线 与抛物线交于A、B两点,且
与抛物线交于A、B两点,且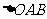 (O为坐标原点)的面积为
(O为坐标原点)的面积为 ,则
,则 等于
等于
A.4 B.2 C.6 D.8
(9)将函数 的图像向左平移
的图像向左平移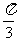 个单位,所得曲线的一部分如图,则
个单位,所得曲线的一部分如图,则 的值分别为
的值分别为

A.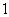 ,
,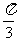 B.
B.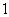 ,
,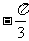 C.
C. ,
,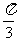 D.
D. ,
,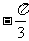
(10)如图,非零向量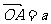 ,
, ,且
,且 ,C为垂足设向量
,C为垂足设向量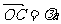 ,则
,则 的值为
的值为

A. B.
B. C.
C.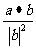 D.
D.
(11)若直线 与圆
与圆 相交于P,Q两点,且点P,Q关于直线
相交于P,Q两点,且点P,Q关于直线 对称,则不等式组
对称,则不等式组 ,表示的平面区域的面积是
,表示的平面区域的面积是
A.1 B.2 C. D.
D.
(12)已知函数 ,若
,若 有且仅有两个实根,则实数
有且仅有两个实根,则实数 的取值范围是
的取值范围是
A.(1,3) B.(1, )
C.[2,3) D.(
)
C.[2,3) D.( ,
, )
)
第Ⅱ卷(非选择题,共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com