
17.(本小题满分12分)
已知点 ,
, ,
,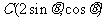 .
.
(1)若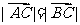 ,求tan
,求tan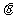 的值;
的值;
(2)若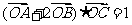 ,其中O为坐标原点,求sin2
,其中O为坐标原点,求sin2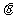 的值.
的值.
16.(本小题满分12分)
已知函数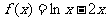
(1)求函数 的单调区间;
的单调区间;
(2)求函数 在点
在点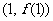 处的切线方程。
处的切线方程。
(二)选做题:第14、15题是选做题,考生只能选做二题,三题全答的,只计算前两题的得分.
14.(坐标系与参数方程)已知圆C的参数方程为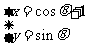 (
( 为参数),则点P (4, 4) 与圆C上的点的最远距离是_________.
为参数),则点P (4, 4) 与圆C上的点的最远距离是_________.
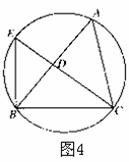
15.(几何证明选讲)如图4所示,圆内接△ABC的∠C的平分线CD延长后交圆于点E,连接BE,已知BD=3,CE=7,BC=5,则线段BE= 。
(一)必做题:第11、12、13题是必做题,每道试题考生都必须做答.
11.函数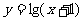 的定义域是
。
的定义域是
。
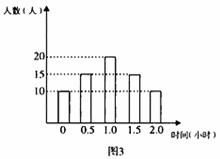
12.某校为了了解学生的体育锻炼情况,随机调查了70名学生,得到他们在某一天各自的体育锻炼时间的数据,结果用如图13所示的条形图表示。根据条形图可得这70名学生这一天平均每人的体育锻炼时间为 小时。
13.已知a为正常数,定义运算“×”,如下:对任意
m,n N*,若m×n=a,则(m+1) ×n=2a,m×(n+1)=a+1.当1×1=1时,则1×10=______,5×10=________.
N*,若m×n=a,则(m+1) ×n=2a,m×(n+1)=a+1.当1×1=1时,则1×10=______,5×10=________.
22.(本小题满分14分)
已知椭圆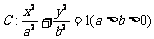 ,点
,点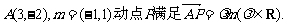
(I)求动点P的轨迹E的方程;
(II)若(I)中曲线E与x轴交于点M,与椭圆C交于A、B两点,且满足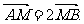 求椭圆C长轴长的取值范围。
求椭圆C长轴长的取值范围。
21.(本小题满分12分)
设函数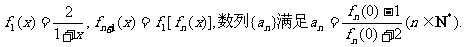
(I)求数列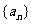 的通项公式;
的通项公式;
(II)若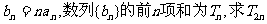 的表达式。
的表达式。
20.(本小题满分12分)
某商场在促销期间规定:商场内所有商品按标价的80%出售;同时,当顾客在该商场内消费满一定金额后,按如下方案获得相应金额的奖券:
|
消费金额的范围(元) |
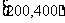 |
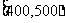 |
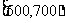 |
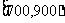 |
|
获得奖券的金额(元) |
30 |
60 |
100 |
130 |
根据上述销售方法,顾客在该商场购物可以获得双重优惠,例如,购买标价为400元的商品,则消费金额为320元,获得的优惠额为:400×0.2+30=110(元),设购买商品得到的优惠率= ,试问:
,试问:
(I)若购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(II)对于标价在[500,800](元)内的商品,顾客购买标价为多少元的商品,可得到不少于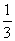 的优惠率?
的优惠率?
19.(本小题满分12分)
已知函数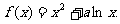
(I)当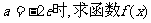 的单调区间和极值;
的单调区间和极值;
(II)若函数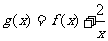 在[1,4]上是减函数,求实数a的取值范围。
在[1,4]上是减函数,求实数a的取值范围。
18.(本小题满分12分)
如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点。
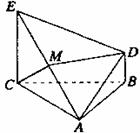
(I)证明:DM∥平面ABC;
(II)证明:CM⊥DE;
17.(本小题满分12分)
在锐角三角形ABC中,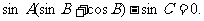
(I)若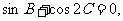 求A、B、C的大小;
求A、B、C的大小;
(II)已知向量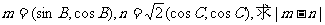 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com