
7.航天员进行的一项太空实验中,要先后实施6个程序A只能出现在第一步或最后一步,程序B和C实施时必须相邻,则实验顺序的编排方法共有 ( )
A.24种 B.48种 C.96种 D.144种
6.设直线m,n是两条不同的直线,α,β是两个不同的平面,则α∥β的一个充分条件是 ( )
A.m∥α,n∥β,m∥n B.m∥α,n⊥β,m∥n
C.m ⊥α,n∥β,m⊥n D.m ⊥α,n⊥β,m∥n
5.在△ABC中,a、b、c分别为三个内角A、B、C所对的边,设向量m=(b-c,c-a),n=(b,c+a),若向量m⊥n,则角A的大小为 ( )
A. B.
B.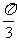 C.
C.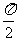 D.
D.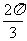
4.函数y=cos(4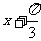 )的图象的相邻两个对称中心间的距离为 ( )
)的图象的相邻两个对称中心间的距离为 ( )
A. B.
B.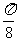 C.
C.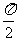 D.π
D.π
3. ( )
( )
A.-1 B.1 C.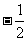 D.
D.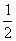
1.已知集合M=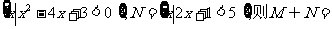 ( )
( )
A. B.
B.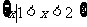 C.
C. D.
D.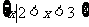 2.已知i为虚数单位,(
2.已知i为虚数单位,( ( )
( )
A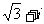 B
B
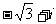 C
C D
D
20.(本小题满分13分)
已知数列{an}为等差数列.
(1)若a1=3,公差d=1,且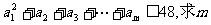 的最大值;
的最大值;
(2)对于给定的正整数m,若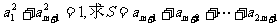 的最大值.
的最大值.
19.(本小题满分13分)已知双曲线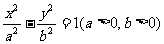 的一条渐近线方程为
的一条渐近线方程为 ,两条准线的距离为l.
,两条准线的距离为l.
(1)求双曲线的方程;
(2)直线l过坐标原点O且和双曲线交于两点M、N,点P为双曲线上异于M,N的一点,且直线PM,PN的斜率均存在,求kPM·kPN的值.
18.(本小题满分13分)
已知将一枚质量不均匀的硬币抛掷一次正面均朝上的概率为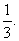
(1)求抛掷这样的硬币三次,恰有两次正面朝上的概率;
(2)抛掷这样的硬币三次后,抛掷一枚质地均匀的硬币一次,求四次抛掷后总共有三次正面朝上的概率.
17.(本小题满分14分)
如图,在四棱锥P-ABCD中,底面ABCD为正方形,△PAB为等边三角形,O为AB中点,且PO⊥AC.
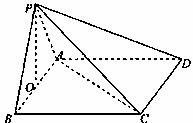
(1)求:平面PAB⊥平面ABCD;
(2)求PC与平面ABCD所成角的大小;
(3)求二面角P-AC-B的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com