
(17)(本小题满分12分)
已知平面内三点A(3,0),B(0,3),C( ,O为坐标原点.
,O为坐标原点.
(1)若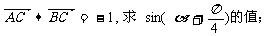
(2)若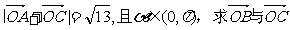 的夹角。
的夹角。
(18)(本小题满分12分)
盒子中装着有标数字1,2,3,4,5的卡片各2张,从盒子中任取3张卡片,每张卡片被取出的可能性都相等,用 表示取出的3张卡片上的最大数字,求:
表示取出的3张卡片上的最大数字,求:
(1)取出的3张卡片上的数字互不相同的概率;
(2)随机变量 的概率分布和数学期望;
的概率分布和数学期望;
(19)(本小题满分12分)
如图,在三棱柱BCE-ADF中,四边形ABCD是正方形,DF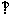 平面ABCD,M、N分别是AB、AC的中点,G是DF上的一点.
平面ABCD,M、N分别是AB、AC的中点,G是DF上的一点.
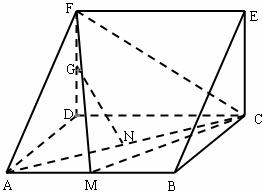
(1)求证:
(2)若FG=GD,求证:GA//平面FMC.
(3)若DF=DA,求二面角F-MC-D的正弦值
(20)(本小题满分12分)
设椭圆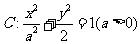 的左右焦点分别为
的左右焦点分别为 、
、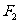 ,
,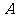 是椭圆
是椭圆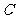 上的一点,且
上的一点,且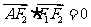 ,坐标原点
,坐标原点 到直线
到直线 的距离为
的距离为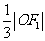 .
.
(Ⅰ)求椭圆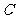 的方程;
的方程;
(Ⅱ)设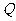 是椭圆
是椭圆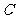 上的一点,过点
上的一点,过点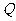 的直线
的直线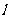 交
交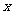 轴于点
轴于点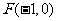 ,交
,交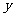 轴于点
轴于点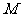 ,若
,若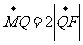 ,求直线
,求直线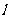 的斜率.
的斜率.
(21)(本小题满分12分)
已知函数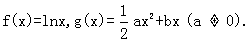
(I)若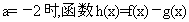 在其定义域是增函数,求b的取值范围;
在其定义域是增函数,求b的取值范围;
(II)在(I)的结论下,设函数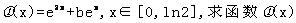 的最小值;
的最小值;
(III)设函数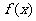 的图象C1与函数
的图象C1与函数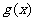 的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
(22) 请考生在A、B、C三题中任选一题作答,如果多做,则按所做的第一题记分。作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑。
(22) A (本小题满分10分)选修4-1:几何证明选讲
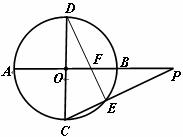
如图所示,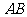 与
与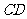 是⊙O的直径,
是⊙O的直径,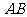
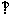
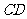 ,
,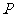 是
是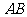 延长线上一点,连
延长线上一点,连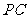 交⊙O于点
交⊙O于点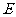 ,连
,连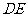 交
交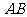 于点
于点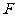 ,若
,若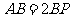 .
.
求证: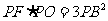
(22) B (本小题满分10分)选修4-4:坐标系与参数方程
在曲线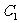 :
: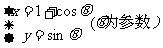 上求一点,使它到直线
上求一点,使它到直线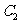 :
: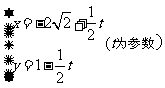 的距离最小,并求出该点坐标和最小距离。
的距离最小,并求出该点坐标和最小距离。
(22) C (本小题满分10分)选修4-5:不等式选讲
若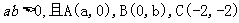 三点共线,求
三点共线,求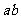 的最小值。
的最小值。
(13)若命题“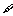 x∈R,使x2+(a-1)x+1<0”是假命题,则实数a的取值范围为
.
x∈R,使x2+(a-1)x+1<0”是假命题,则实数a的取值范围为
.
(14)在区间[1, 5 ]上分别取一个实数,记为m
,则方程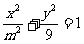 表示焦点在x轴上的椭圆的概率是____________________
表示焦点在x轴上的椭圆的概率是____________________
(15)若三角形内切圆半径为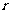 ,三边长分别为
,三边长分别为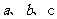 ,则三角形的面积
,则三角形的面积 ,根据类比思想,若四面体内切球半径为
,根据类比思想,若四面体内切球半径为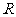 ,其四个面的面积分别为
,其四个面的面积分别为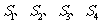 ,则四面体的体积
,则四面体的体积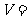 ________
________
(16)某小卖部为了了解热茶销售量y(杯)与气温x(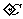 )之间的关系,随机统计了某4天卖出的热茶的杯数与当天气温,并制作了对照表:
)之间的关系,随机统计了某4天卖出的热茶的杯数与当天气温,并制作了对照表:
气温x(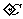 ) ) |
18 |
13 |
10 |
-1 |
|
杯数y |
24 |
34 |
38 |
64 |
由表中数据算得线性回归方程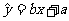 中的
中的 ,预测当气温为
,预测当气温为 时,热茶销售量为________杯.(回归系数
时,热茶销售量为________杯.(回归系数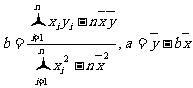 )
)
22.(14分)如图,在平面直角坐标系中,N为圆A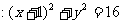 上的一动点,点B(1,0),点M是BN中点,点P在线段AN上,且
上的一动点,点B(1,0),点M是BN中点,点P在线段AN上,且
(1)求动点P的轨迹方程;
(2)试判断以PB为直径的圆与圆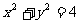 的位置关系,并说明理由。
的位置关系,并说明理由。

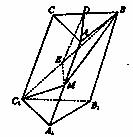
21.(12分)在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1⊥底面ABC。
(1)若D是BC的中点,求证:AD⊥CC1;
(2)过侧面BB1C1C的对角线BC1的平面交侧棱于M,若AM=MA1,求证:截面MBC1⊥侧面BB1C1C;
(3)AM=MA1是截面MBC1⊥平面BB1C1C的充要条件吗?请说明理由。
20.(12分)已知各项均为正数的数列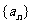 的前n项和为Sn,且
的前n项和为Sn,且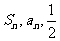 成等差数列。
成等差数列。
(1)求数列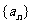 的通项公式;
的通项公式;
(2)若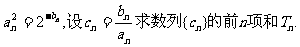
19.(12分)已知函数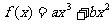 的图象经过点M(1,4),曲线在点M处的切线恰好与直线
的图象经过点M(1,4),曲线在点M处的切线恰好与直线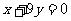 垂直。
垂直。
(1)求实数a,b的值;
(2)若函数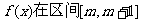 上单调递增,求m的取值范围。
上单调递增,求m的取值范围。
18.(12分)对某电子元件进行寿命追踪调查,情况如下:
|
寿命(h) |
100-200 |
200-300 |
300-400 |
400-500 |
500-600 |
|
个数 |
20 |
30 |
80 |
40 |
30 |
(1)列出频率分布表;
(2)画出频率分布直方图;
(3)估计电子元件寿命在100-400h以内的概率;
(4)估计电子元件寿命在400h以上的概率。
17.(12分)已知向量
(1)当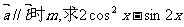 的值;
的值;
(2)求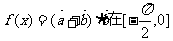 上的值域。
上的值域。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com