
7.如果函数 在闭区间[一1,2]上有反函数,那么实数
在闭区间[一1,2]上有反函数,那么实数 的取值范围是
的取值范围是
A.(一∞,2] B.(一∞,一4]∪[2,+∞)
C.[一2,+∞) D.(-∞,一2]∪[4,+∞)
6.在平面直角坐标系中,不等式组 表示的平面区域面积是
表示的平面区域面积是
A.3 B.6 C. D.9
D.9
5.设圆 上有且只有两个点到直线
上有且只有两个点到直线 的距离等于1,则圆的半径r的取值范围是
的距离等于1,则圆的半径r的取值范围是
A. B.
B. C.
C. D.
D.
4.已知 为第二象限的角,且
为第二象限的角,且 ,则
,则 值为
值为
A. B.
B.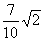 C.
C. D.
D.
3.已知向量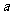 与
与 的夹角为l20°,若向量
的夹角为l20°,若向量 ,且
,且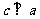 ,则
,则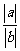 值为
值为
A.2 B.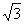 C.
C. D.
D.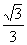
2.已知函数 ,则
,则 为
为
A. B.
B. C.
C. D.
D.
1.已知函数 的定义域为[一1,1],记集合M=[一1,1],
的定义域为[一1,1],记集合M=[一1,1], 的值域为集合N,则M∩N为
的值域为集合N,则M∩N为
A.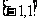 B.[
B.[ ] C.[0,1] D.[0,
] C.[0,1] D.[0,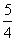 ]
]
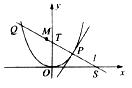
21.(本小题满分14分)如图所示,P是抛物线C: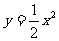 上一点,直线
上一点,直线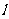 过点P并与抛物线C在点P的切线垂直,
过点P并与抛物线C在点P的切线垂直,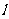 与抛物线C相交于另一点Q.
与抛物线C相交于另一点Q.
(1)当点P的横坐标为2时,求直线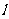 的方程;
的方程;
(2)当点P在抛物线C上移动时,求线段PQ中点M的轨迹方程,并求点M到 轴的最短距离.
轴的最短距离.
20.(本小题满分13分)已知 是二次函数,不等式
是二次函数,不等式 的解集是(0,5),且
的解集是(0,5),且 在区间[一1,4]上的最大值是l2.
在区间[一1,4]上的最大值是l2.
(1)求 的解析式;
的解析式;
(2)是否存在自然数优使得方程 在区间(m,m+1)内有且只有两个不等的实数根?若存在,求出m的取值范围;若不存在,说明理由.
在区间(m,m+1)内有且只有两个不等的实数根?若存在,求出m的取值范围;若不存在,说明理由.
19.(本小题满分12分)一种化工产品的单价随着其纯度的提高而提高.某化学公司计划要用单价为A元/kg的原料100 kg进行提纯.每次提纯后产品的总价值按如下方法计算:每提纯一次,产品的重量将减少2%,随着产品纯度的提高,提纯后产品的“初步单价”(即未扣除加工费时的“单价”)是提纯前单价的1.3倍,在此计算结果的基础上每提纯一次需要扣除的加工费用是本次提纯前总价值的7.4%(注:本次提纯后的总价值=本次提纯后的重量×本次提纯后的单价).
(1)问第一次提纯后产品的总价值是多少元?
(2)求使这种产品总价值翻一番的最小提纯次数 的值.(参考数据:lg2=0.3010,lg3=0.4771)
的值.(参考数据:lg2=0.3010,lg3=0.4771)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com