
21.(本小题满分14分)点P是以F1、F2为焦点的双曲线E: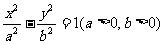 上的一点,已知PF1⊥PF2,|PF1|一2|PF2|,O为坐标原点.
上的一点,已知PF1⊥PF2,|PF1|一2|PF2|,O为坐标原点.
(1)求双曲线的离心率e;
(2)过点P作直线分别与双曲线两渐近线相交于P1、P2两点,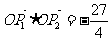 ,
, ,求双曲线E的方程;
,求双曲线E的方程;
(3)若过点Q(m,0)(m为非零常数)的直线 与(2)中的双曲线E相交于不同于双曲线顶点的两点M、N且
与(2)中的双曲线E相交于不同于双曲线顶点的两点M、N且 (
(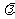 为非零实数),问在
为非零实数),问在 轴上是否存在定点G,使
轴上是否存在定点G,使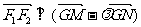 ?若存在,求出所有这种定点G的坐标;若不存在,请说明理由.
?若存在,求出所有这种定点G的坐标;若不存在,请说明理由.
20.(本小题满分13分)已知函数 。
。
(1)求证:函数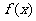 是偶函数;
是偶函数;
(2)判断函数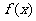 分别在区间(0,2]、[2,+
分别在区间(0,2]、[2,+ )上的单调性,并加以证明;
)上的单调性,并加以证明;
(3)若1≤|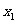 |≤4,1≤|
|≤4,1≤| |≤4,求证:|
|≤4,求证:| |≤1.
|≤1.
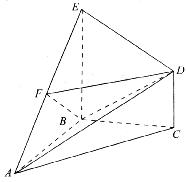
19.(本小题满分12分)如图所示,在几何体ABCDE中,△ABC是等腰直角三角形,△ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点.
(1)证明:DF//平面ABC;
(2)求AB与平面BDF所成角的大小.
18.(本小题满分12分)某工厂生产某种产品,已知该产品的产量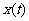 与每吨产品的价格P(元/t)之间关系为P=24200一
与每吨产品的价格P(元/t)之间关系为P=24200一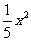 ,且生产
,且生产 t的成本为R=50000+200
t的成本为R=50000+200 元.问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入一成本)
元.问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入一成本)
17.(本小题满分12分)设函数 ,不等式
,不等式 的解集为(一1,2),试求不等式
的解集为(一1,2),试求不等式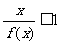 的解集.
的解集.
16.(本小题满分12分)已知△ABC的面积S满足 ≤S≤3,且满足
≤S≤3,且满足 .
. =6.
=6.
(1)求角B的取值范围;
(2)若 与
与 的夹角为
的夹角为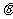 ,求
,求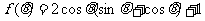 的最小值.
的最小值.
15.某汽车站每天均有3辆开往北京的分为上、中、下等级的客车,某天袁先生准备在该汽车站乘车前往北京办事,但他不知道客车的车况,也不知道发车的顺序,为了尽可能乘上上等车,他采取如下策略:先放过第一辆车,如果第二辆比第一辆好,则上第二辆,否则上第三辆,那么他乘上上等车的概率为_____________.
14.当 、
、 满足条件
满足条件 (
(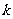 为常数)时,能使
为常数)时,能使 的最大值为12的
的最大值为12的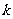 的值是_________.
的值是_________.
13.设{ }是公比为q的等比数列,Sn是它的前n项和,若{Sn}是等差数列,则q=_______。
}是公比为q的等比数列,Sn是它的前n项和,若{Sn}是等差数列,则q=_______。
12.已知 ,
, ,则tan
,则tan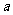 =_____________.
=_____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com