
6.直线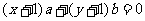 与圆
与圆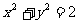 的位置关系是
的位置关系是
A.相交 B.相离 C.相切或相离 D.相切或相交
5.指数函数 且
且 )的图像如图所示,那么不等式
)的图像如图所示,那么不等式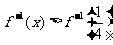 的解集为
的解集为
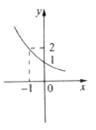
A.(0, ) B.(0,4) C.(
) B.(0,4) C.( ,+∞) D.(4,+∞)
,+∞) D.(4,+∞)
4.已知 、
、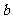 为异面直线,则:
为异面直线,则:
(1)经过直线 ,存在唯一平面
,存在唯一平面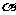 ,使
,使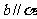 ;
;
(2)经过直线 ,若存在平面
,若存在平面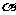 ,使
,使 ,则
,则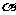 唯一;
唯一;
(3)不存在直线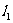 、
、 、…、
、…、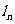 ,使
,使 、
、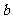 、
、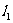 、
、 、…、
、…、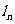 中任意两条直线为异面直线,上述命题中,真命题的个数为
中任意两条直线为异面直线,上述命题中,真命题的个数为
A.0个 B.1个 C.2个 D.3个
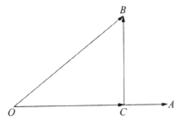
3.如图所示,非零向量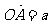 ,
, ,且BC⊥OA,C为垂足,设向量
,且BC⊥OA,C为垂足,设向量 ,则
,则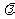 的值为
的值为
A.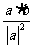 B.
B. C.
C. D.
D.
2.若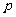 、
、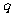 ∈R,则
∈R,则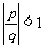 成立的一个充分不必要条件是
成立的一个充分不必要条件是
A. B.
B.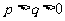 C.
C.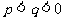 D.
D.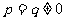
1.落在平静水面上的石头,使水面产生同心圆形波纹,在持续的一段时间内,若最外一圈波的半径的变化率总是6 m/s,则在2 s末扰动水面面积的变化率为
A.288 m2/s B.144
m2/s B.144 m2/s C.108
m2/s C.108 m2/s D.172
m2/s D.172 m2/s
m2/s
21.(本小题满分14分)二次函数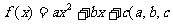 ∈Z)的图像按向量
∈Z)的图像按向量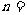 (-1,0)平移后关于y轴对称,方程
(-1,0)平移后关于y轴对称,方程 的两根为
的两根为 、
、 ,且
,且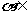 (0,2),
(0,2),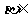 (2,4),
(2,4),
(1)求函数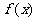 的解析式;
的解析式;
(2)设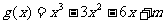 ,若存在常数
,若存在常数 ,使得函数
,使得函数 、
、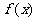 在区间[-2,2]上的图像分别在直线
在区间[-2,2]上的图像分别在直线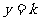 的上方和下方,试求实数m的取值范围.
的上方和下方,试求实数m的取值范围.
20.(本小题满分13分)已知抛物线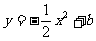 ,点A、B及P(2,4)都在抛物线上,并且直线PA、PB的倾斜角互补.
,点A、B及P(2,4)都在抛物线上,并且直线PA、PB的倾斜角互补.
(1)直线AB的斜率是否为定值?如果是,请加以证明;若不是,请说明理由.
(2)当直线AB在y轴上的截距大于零时,求△PAB面积的最大值.
19.(本小题满分12分)如图所示.三棱柱A。B。C1-ABC的侧面BCC1B1是菱形,∠CBB1=60°,AB⊥面BCClB1,AB=3,BB1=4.
(1)求证:BlC⊥AC1;
(2)若D是AB的中点,求二面角D-CC1-B的平面角的余弦值.

18.(本小题满分12分)已知数列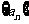 是公比为q的等比数列,S
是公比为q的等比数列,S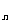 是其前
是其前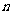 项和,且S
项和,且S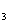 ,S
,S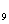 ,S
,S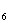 成等差数列.
成等差数列.
(1)求证: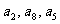 也成等差数列.
也成等差数列.
(2)判断以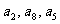 为前三项的等差数列的第四项是否也是数列
为前三项的等差数列的第四项是否也是数列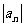 中的一项,若是,求出这一项;若不是,请说明理由.
中的一项,若是,求出这一项;若不是,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com