
4.设某等差数列的首项为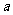 (
(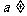 0),第二项为
0),第二项为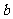 ,则这个数列中有一项为0的充要条件是
,则这个数列中有一项为0的充要条件是
A. 是正整数 B.
是正整数 B.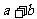 是正整数 C.
是正整数 C.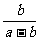 是正整数 D.
是正整数 D.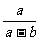 是正整数
是正整数
3.把一正态曲线C1沿着横轴方向向右移动2个单位,得到一条新的曲线C2,下列说法不正确的是
A.曲线C2仍是正态曲线
B.曲线C1、C2的最高点的纵坐标相等
C.以曲线C2为概率密度曲线的总体的方差比以曲线C1为概率密度曲线的总体的方差大2
D.以曲线C2为概率密度曲线的总体的期望比以曲线C1为概率密度曲线的总体的期望大2
2.若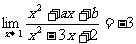 ,则复数
,则复数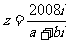 在复平面内对应的点位于
在复平面内对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
1.设全集U=R,M={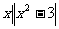 ≤1},N={
≤1},N={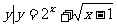 },那么M∩(
},那么M∩(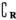 N)=
N)=
A.[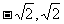 ] B.[一2,2]
] B.[一2,2]
C.[-2,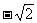 ]∪[
]∪[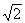 ,2)
D.[一2,
,2)
D.[一2,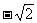 ]∪[
]∪[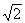 ,2]
,2]
21.(本小题满分14分)
已知函数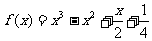 .
.
(1)证明:存在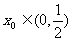 ,使
,使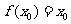 ;
;
(2)设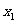 =0,
=0,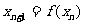 ,
,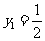 ,
,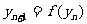 ,其中
,其中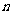 =1,2,…,证明:
=1,2,…,证明: ;
;
(3)证明: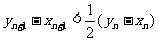 .
.
20.(本小题满分13分)
已知A(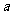 ,
,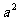 )为抛物线
)为抛物线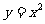 任意一点,直线
任意一点,直线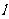 为过点A的切线,设直线
为过点A的切线,设直线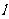 交
交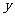 轴于点B,
轴于点B,
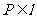 .且
.且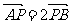 .
.
(1)当A点运动时,求点P的轨迹方程;
(2)求点C(0,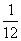 )到动直线
)到动直线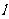 的最短距离,并求此时
的最短距离,并求此时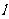 的方程.
的方程.
19.(本小题满分12分)
一种电脑屏幕保护画面只有符号“○”和“×”随机地反复出现,每秒钟变化一次,每次变化只出现“○”和“×”之一,其中出现“○”的概率为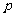 ,出现“×”的概率为
,出现“×”的概率为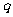 .若第
.若第 次出现“○”,则
次出现“○”,则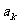 =1;出现“×”,则
=1;出现“×”,则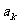 =-1.令
=-1.令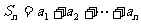 .
.
(1)当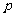 =
=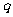 =
=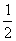 时,记
时,记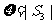 ,求
,求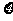 的分布列及数学期望;
的分布列及数学期望;
(2)当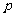 =
=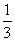 ,
,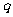 =
=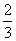 时,求S8=2且Si≥0(i=1,2,3,4)的概率.
时,求S8=2且Si≥0(i=1,2,3,4)的概率.
18.(本小题满分12分)
如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1上底面ABC,∠A1AC=60°.
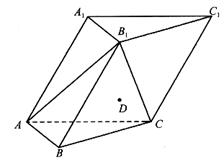
(1)求侧棱AA1与平面AB1C所成角的大小;
(2)已知点D满足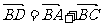 ,在直线AA1上是否存在点P,使DP∥平面AB1C?若存在,请确定点P的位置;若不存在,请说明理由.
,在直线AA1上是否存在点P,使DP∥平面AB1C?若存在,请确定点P的位置;若不存在,请说明理由.
17.(本小题满分12分)
我国加入WTO后,根据达成的协议,若干年内某产品关税与市场供应量P的关系允许近似地满足: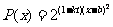 ,其中
,其中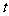 为关税的税率,且
为关税的税率,且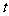 ∈(0,
∈(0,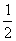 ),
),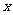 为市场价格,b、k为正常数,当
为市场价格,b、k为正常数,当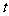 =
=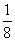 时的市场供应量曲线如图所示.
时的市场供应量曲线如图所示.
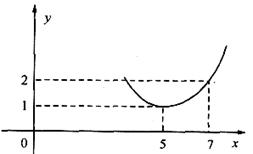
(1)根据图像求k、b的值;
(2)若市场需求量为Q,它近似满足Q(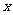 )=
)=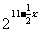 ,当P=Q时的市场价格称为市场平衡价格,为使市场平衡价格不低于9元,求税率
,当P=Q时的市场价格称为市场平衡价格,为使市场平衡价格不低于9元,求税率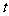 的最小值.
的最小值.
16.(本小题满分12分)
已知向量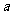 =(2,2),向量b与向量
=(2,2),向量b与向量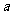 的夹角为
的夹角为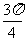 ,且
,且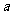 .b=-2.
.b=-2.
(1)求向量b;
(2)向量c=(cosA,2cos2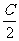 ),其中A、C是△ABC的内角,若三角形的三个内角A、B、C依次成等差数列,且向量b与
),其中A、C是△ABC的内角,若三角形的三个内角A、B、C依次成等差数列,且向量b与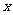 轴垂直,试求|b+c|的取值范围.
轴垂直,试求|b+c|的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com