
22.(本题满分14分)
己知直线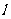 :
: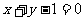 与椭圆C:
与椭圆C: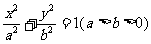 相交于A,B两点,且
相交于A,B两点,且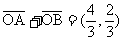
(Ⅰ)求椭圆C的离心率;
(Ⅱ)若椭圆经过抛物线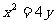 的焦点,且过点M(0,2)的直线与椭圆交于不同的两点E,F,试求△OME与△OMF面积之比的取值范围。
的焦点,且过点M(0,2)的直线与椭圆交于不同的两点E,F,试求△OME与△OMF面积之比的取值范围。
21、(本小题满分12分)
已知函数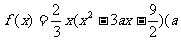 ∈R)
∈R)
(Ⅰ)若函数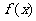 图像上点P(1,
图像上点P(1,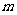 )处的切线方程为
)处的切线方程为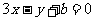 ,求
,求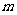 的值.
的值.
(Ⅱ)若函数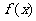 在(1,2)内是增函数,求
在(1,2)内是增函数,求 的取值范围.
的取值范围.
20.(本小题满分12分)
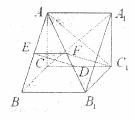
如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,AA1=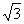 ,
,
证明:(Ⅰ)A1C⊥平面AB1C1;
(Ⅱ)若D是棱CC1的中点,在棱AB上是否存在一点E,使DE//平面AB1C1?证明你的结论.
19.(本大题满分12分)
某旅行社组团去风景区旅游,若每团人数在30人或30人以下,飞机票每张收费900元;若每团人数多于30人,则给予优惠,每多1人,机票每张减少10元,直至每张降为450元为止,每团乘飞机,旅行社需付给航空公司包机费15000元.
(Ⅰ)写出飞机票的价格关于人数的函数;
(Ⅱ)每团人数为多少时,旅行社可获得最大利润?
18.(本题满分12分)
已知数列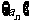 的前
的前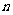 项和为S
项和为S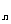 ,且满足
,且满足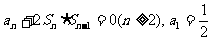 ,
,
(Ⅰ)求证: 成等差数列;(Ⅱ)求
成等差数列;(Ⅱ)求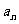 的表达式。
的表达式。
17.(本题满分12分)
已知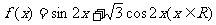 .
.
(Ⅰ)求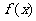 的最小正周期;
的最小正周期;
(Ⅱ)当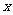 为何值时,
为何值时,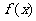 取得最大值,最大值是多少?
取得最大值,最大值是多少?
(Ⅲ)求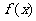 的单调递减区间
的单调递减区间
16.若方程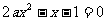 在(0,1)内恰有一解,则
在(0,1)内恰有一解,则 的取值范围是
.
的取值范围是
.
15.已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则该双曲线的离心率 为 .
14.已知两圆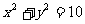 和
和 相交于A,B两点,则直线AB的方程 是
.
相交于A,B两点,则直线AB的方程 是
.
13.一个总体含有100个个体,以简单随机抽样方式从该总体中抽取一个容量为5的样本,则指定的某个个体被抽到的概率为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com