20．(本小题满分12分)

抛物线的准线与坐标轴交于A点，过A作直线与抛物线交于M、N两点，点B在抛物线的对称轴上，且。

　 (Ⅰ)求的范围；

　 (Ⅱ)是否存在这样的点B，使得△BMN为等腰直角三角形，且∠B=90º。若存在，求出点B；若不存在，说明理由。

19．(本小题满分12分)

在三棱柱ABC-A₁B₁C₁中，底面是边长为的正三角形，点A₁在底面ABC上的射影O恰是BC的中点。

　　 (Ⅰ)求证：A₁A⊥BC；

　　 (Ⅱ)当侧棱AA₁和底面成45º角时，求二面角A₁-AC-B的大小

　　 (Ⅲ)若D为侧棱A₁A上一点，当为何值时，BD⊥A₁C₁。

18．(本小题满分12分)

　 在一个盒子中，放有标号分别为1，2，3的三张卡片，现从这个盒子中，有放回地先 后抽得两张卡片的标号分别为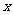、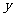，记。

　 (Ⅰ)求随机变量的最大值，并求事件“取得最大值”的概率；

　 (Ⅱ)求随机变量的分布列和数学期望。

17．(本小题满分12分)

已知，，

　 (Ⅰ)当时，求函数的最小正周期；

　 (Ⅱ)当，，，是锐角时，求的值。

16．已知正三棱锥S-ABC内接于半径为6的球，过侧棱SA及球O的平面截三棱锥及球面所得截面如下图，则此三棱锥的侧面积为　　　　　　 。

15．现准备将6台型号相同的电脑分配给5所小学，其中A、B两所希望小学每个学校至少2台，其他小学允许l台也没有，则不同的分配方案共有　　　　　　 种(用数字作答)。

14．下面流程图中，语句1(语句1与i无关)将被执行的次数为　　　　　　 。

13．已知二项式的展开式的第6项为常数项，则n=　　　　　　 。

12．已知C为线段AB上的一点，P为直线AB外一点，满足，，，I为PC上一点，且，则的值为

A．1　　 　　　　　　　　　　 B．2 　　　　　　　　　　　　 C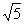． 　　　　　　　　　　　 D．

第Ⅱ卷(非选择题　 共90分)

11．某人为了观看2008年奥运会，从2001年起每年5月10日到银行存入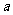元定期储蓄，若年利率为p且保持不变，并且每年到期的存款及利息均自动转为新一年定期，到2008年将所有的存款和利息全部取回，则可取回的钱的总数(元)为　

A．　　　　　　　　　　　　　　　　　　　　　　　　 B．

C．　　　　　　　　 　　　　　　　 D．