
20.(本小题满分12分)
如图,正三棱锥O-ABC的三条侧棱OA、OB、OC两两垂直,且长度均为2,E、F分别是AB、AC的中点,H是EF的中点,过EF的一个平面与侧棱OA、OB、OC或其延长线分别相交于A1、B1、C1,已知OA1=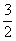 .
.
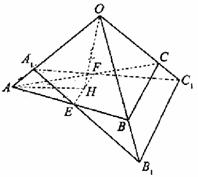
(1)证明:B1C1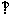 平面OAH;
平面OAH;
(2)求二面角O-A1B1-C1的大小.
19.(本小题满分12分)
等差数列{an}各项均为正整数,a1=3,前n项和为Sn,等比数列{bn}中,b1=1,且b2S2=64,{ban}是公比为64的等比数列.
(1)求an与bn;
(2)证明: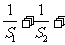 …+
…+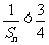 .
.
18.(本小题满分12分)
因冰雪灾害,某柑桔基地果林严重受损,为此有关专家提出两种拯救果树的方案,每种方案都需分两年实施.若实施方案一,预计第一年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4;第二年可以使柑桔产量为第一年产量的1.25倍、1.0倍的概率分别是0.5、0.5.若实施方案二,预计第一年可以使柑桔产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5;第二年可以使柑桔产量为第一年产量的1.2倍、1.0倍的概率分别是0.4、0.6.实施每种方案第一年与第二年相互独立,令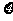 I(i=1,2)表示方案i实施两年后柑桔产量达到灾前产量的倍数.
I(i=1,2)表示方案i实施两年后柑桔产量达到灾前产量的倍数.
(1)写出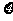 1、
1、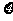 2的分布列;
2的分布列;
(2)实施哪种方案,两年后柑桔产量超过灾前产量的概率更大?
(3)不管哪种方案,如果实施两年后柑桔产量达不到、恰好达到、超过灾前产量,预计利润分别为10万元、15万元、20万元.问实施哪种方案的平均利润更大?
17.(本小题满分12分)
在△ABC中,a、b、c分别为角A、B、C所对的边长,a=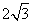 ,tan
,tan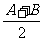 +tan
+tan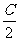 =4,sinBsinC=cos2
=4,sinBsinC=cos2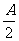 .求A、B及b、c.
.求A、B及b、c.
16.如图1,一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实习装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水平也恰好过点P(图2).
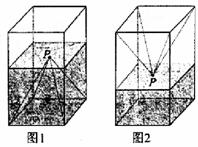
有下列四个命题:
A.正四棱锥的高等于正四棱柱高的一半
B.将容器侧面水平放置时,水面也恰好过点P
C.任意摆放该容器,当水面静止时,水面都恰好经过点P
D.若往容器内再注入a升水,则容器恰好能装满其中真命题的代号是:________(写出所有真命题的代号).
15.过抛物线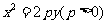 的焦点F作倾斜角为30°的直线,与抛物线分别交于A、B两点(点A在y轴左侧),则
的焦点F作倾斜角为30°的直线,与抛物线分别交于A、B两点(点A在y轴左侧),则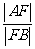 =__________.
=__________.
14.不等式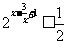 的解集为_________.
的解集为_________.
13.直角坐标平面内三点A(1,2)、B(3,-2)、C(9,7),若E、F为线段BC的三等分点,则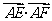 =___________.
=___________.
12.已知函数f(x)= 2mx2-2(4-m)x+1,g(x)=mx,若对于任一实数x,f(x)与g(x)的值至少有一个为正数,则实数m的取值范围是
A.(0,2) B.(0,8) C.(2,8) D.(-∞,0)
第Ⅱ卷
第Ⅱ卷2页,须用黑色墨水签字笔在答题卡上书写作答.若在试题卷上作答,答案无效.
11.电子钟一天显示的时间是从00:00到23:59,每一时刻都由四个数字组成,则一天中任一时刻显示的四个数字之和为23的概率为
A.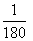 B.
B.
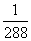 C.
C.
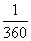 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com