
18.(本小题满分12分)
因冰雪灾害,某某枯基地果林严重损,为此有关专家提出一种拯救果树的方案,该方案需分两年施且相互独立,该方案预计第一年可以使柑桔产量恢复到灾前1.0倍、0.9倍、0.8倍的概率分别是0.2.0.4.0.4;第二年可以使柑桔产量为第一年产量的1.5倍、1.25倍、1.0倍的概率分别是0.3、0.3、0.4.
(1) 求两年后柑桔产量恰好达到灾前产量的概率;
(2) 求两年后柑桔产量超过灾前产量的概率;
17.(本小题满分12分)
已知tanα=-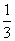 ,cosβ=
,cosβ=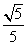 ,α,β
,α,β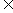 (0,π),
(0,π),
(1) 求tan(αβ)的值;
(2)
求函数f(x)=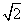 sin(x-α)+cos(x+β)的最大值.
sin(x-α)+cos(x+β)的最大值.
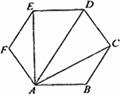
16.如图,正六边形ABCDEF中,有下列四个命题:
A.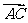 +
+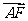 =2
=2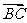
B.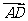 =2
=2 +2
+2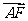
C.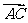 ·
·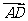 =
=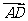 ·
·
D.(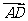 ·
·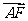 )
)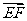 =
=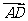 (
(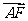 ·
·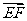 )
)
其中真命题的代号是 .(写出所有真命题的代号)
15.连结球面上两点的线段称为球的一条弦.半径为4的球的两条弦AB、CD的长度分别等于2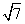 、4
、4 ,每条弦的两端都在球面上运动,则两弦中点之间距离的最大值为 .
,每条弦的两端都在球面上运动,则两弦中点之间距离的最大值为 .
14.已知双曲线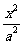 -
-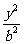 =1(a>0,b>0)的两条渐近线方程为y=±
=1(a>0,b>0)的两条渐近线方程为y=±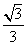 x,若顶点到渐近线的距离为1,则双曲线方程为 .
x,若顶点到渐近线的距离为1,则双曲线方程为 .
13.不等式2x2+2x≤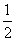 的解集为 .
的解集为 .
12.已知函数f(x)=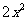 +(4-m)x+4-m,g(x)=mx,若对于任一实数xf(x)与g(x)的值到少有一个为正数,则实数m的取值范围是
+(4-m)x+4-m,g(x)=mx,若对于任一实数xf(x)与g(x)的值到少有一个为正数,则实数m的取值范围是
A.[-4,4] B.(-4,4) C.(-∞,4) D.(-∞,-4)
第Ⅱ卷
第Ⅱ卷2面,须用黑色水签字笔在答题卡上书写作答,在试题卷上作答,答案无效。
11.电子钟一天显示的时间是从00:00到23:59,每一时刻都由四个数字组成,则一天中任一时刻显示的四个数字之和为23的概率为
A.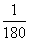 B.
B.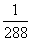 C.
C.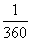 D.
D.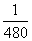
10.函数y=tanx+sinx-|tanx-sinx|在区间(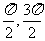 )内的图象大致是
)内的图象大致是
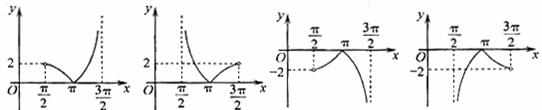
A B C D
9.设直线m与平面α相交但不垂直,则下列说法中正确的是
A. 在平面α内有且只有一条直线与直线m垂直
B. 过直线m有且只有一个平面与平面α垂直
C. 与直线m垂直的直线不可能与平面α平行
D. 与直线m平行的平面不可能与平面α垂直
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com