
8.在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD交于点F.若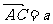 ,,
,, ,则
,则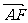 =
=
A.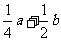 B.
B.
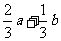 C.
C.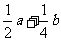 D.
D.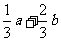
7.设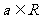 ,若函数y=eax+3x,x
,若函数y=eax+3x,x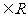 有大于零的极值点,则
有大于零的极值点,则
A. B.
B.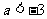 C.
C.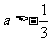 D.
D. 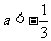
6.已知命题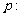 所有有理数都是实数,命题
所有有理数都是实数,命题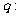 正数的对数都是负数,则下列命题中为真命题的是
正数的对数都是负数,则下列命题中为真命题的是
A.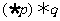 B.
B.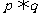 C.
C.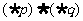 D.
D.
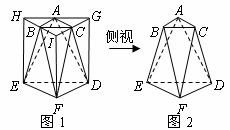
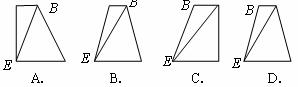
5.将正三棱柱截去三个角(如图1所示啊,A,B,C分别是△GHI三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为
4.若变量x,y满足 则z=3x+2y的最大值是
则z=3x+2y的最大值是
A.90 B.80 C.70 D.40
3.某校共有学生2000名,各年级男、女生人数如表1.已知在全校学生中随机抽取1名,抽到二年级女生的概率是0.19.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为
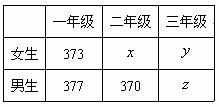 表1
表1
A.24 B.18 C.16 D.12
2.记等差数列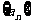 的前n项和为Sn,若
的前n项和为Sn,若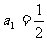 ,Sn=20,则S6=
,Sn=20,则S6=
A.16 B.24 C.36 D.48
1.已知0<a<2,复数z的实部为a,虚部为1,则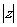 的取值范围是
的取值范围是
A.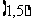 B.
B.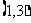 C.
C.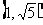 D.
D.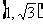
21.(本小题满分14分)
设数列{an}满足a1=1, a2=2, an=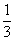 (an-1+2an-2)(n=3,4,…),数列{bn}满足b1=1,bn(n=2,3,…)是非零整数,且对任意的正整数m和自然数k,都有-1
(an-1+2an-2)(n=3,4,…),数列{bn}满足b1=1,bn(n=2,3,…)是非零整数,且对任意的正整数m和自然数k,都有-1 bm+bm+1+…+bm+1
bm+bm+1+…+bm+1 1.
1.
(1)求数列{an}和{bn}的通项公式;
(2)记cn=nanbn(n=1,2,…),求数列{cn}的前n项和Sn
20.(本小题满分14分)
设b 0,椭圆方程为
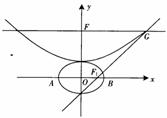
0,椭圆方程为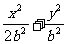 =1,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点F1.
=1,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点F1.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设A1B分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点P,使得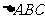 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com