
4.函数f(x)=x3+sinx+1(x∈R),若f(a)=2,则f(-a)的值为
A.3 B.0 C.-1 D.-2
3.设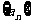 是等比数列,若a2=3,a7=13,则数列
是等比数列,若a2=3,a7=13,则数列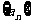 前8项的和为
前8项的和为
A.128 B.80 C.64 D.56
2.“a=1”是“直线x+y=0和直线x-ay=0互相垂直”的
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
1.若集合A={x|x2-x<0},B={x|0<x<3},则A∩B等于
A.{x|0<x<1} B.{x|0<x<3}
C.{x|1<x<3}
D.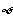
(17)(本小题满分12分)
已知函数f(x)=cos(2x-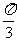 )+2sin(x-
)+2sin(x-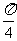 )sin(x-
)sin(x-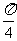 ).
).
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数f(x)在区间[-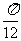 ,
,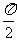 ]上的值域.
]上的值域.
(18)(本小题满分12分)
在某次普通话测试中,为测试字发音水平,设置了10张卡片,每张卡片上印有一个汉字的拼音,其中恰有3张卡片上的拼音带有后鼻音“g”.
(Ⅰ)现对三位被测试者先后进行测试,第一位被测试者从这10张卡片中随机抽取1张,测试后放回,余下2位的测试,也按同样的方法进行,求这二位被测试者抽取的卡片上,拼音都带有后鼻音“g”的概率;
(Ⅱ)若某位被测试者从这10张卡片中一次随机抽取3张,求这3张卡片上,拼音带有后鼻音“g”的卡片不少于2张的概率.
(19)(本小题满分12分)
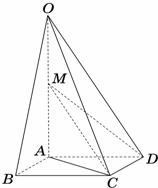
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的菱形,∠ABC=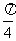 ,OA⊥底面ABCD,OA=2,M为OA的中点.
,OA⊥底面ABCD,OA=2,M为OA的中点.
(Ⅰ)求异面直线AB与MD所成角的大小;
(Ⅱ)求点B到平面OCD的距离.
(20)(本小题满分12分)
已知函数f(x)= 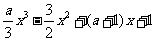 ,其中a为实数.
,其中a为实数.
(Ⅰ)已知函数f(x)在x=1处取得极值,求a的值;
(Ⅱ)已知不等式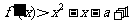 对任意
对任意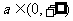 都成立,求实数x的取值范围.
都成立,求实数x的取值范围.
(21)(本小题满分12分)
设数列{an}满足a1=a,
an+1=can+1-c, 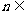 N*,其中a,c为实数,且c
N*,其中a,c为实数,且c 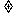 0.
0.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设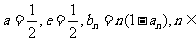 N*,求数列{bn}的前n项和Sn;
N*,求数列{bn}的前n项和Sn;
(Ⅲ)若0<an<1对任意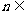 N*成立,证明0<c
N*成立,证明0<c 1.
1.
(22)(本小题满分14分)
已知椭圆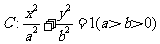 ,其相应于焦点F(2,0)的准线方程为x=4.
,其相应于焦点F(2,0)的准线方程为x=4.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知过点F1(-2,0)倾斜角为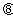 的直线交椭圆C于A,B两点.
的直线交椭圆C于A,B两点.
求证: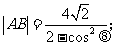
(Ⅲ)过点F1(-2,0)作两条互相垂直的直线分别交椭圆C于点A、B和D、E,求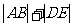 的最小值.
的最小值.
(13)函数f(x)=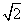
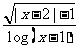 的定义域为 .
的定义域为 .
(14)已知双曲线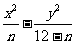 =1的离心率为
=1的离心率为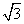 ,则n=
,则n=
(15)在数列{an}中,an=4n-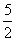 ,a1+ a2+…+ aa=an2+bn,n∈N*,其中a,b为常数,则ab= .
,a1+ a2+…+ aa=an2+bn,n∈N*,其中a,b为常数,则ab= .
(16)已知点A,B,C,D在同一球面上,AB⊥平面BCD,BC⊥CD.若AB=6,AC=2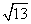 ,AD=8,则B,C两点间的球面距离是 .
,AD=8,则B,C两点间的球面距离是 .
(1)若A为全体正实数的集合,B=(-2,-1,1,2),则下列结论中正确的是
A.A∩B={-2,-1} B.(CRA)∪B=(-∞,0)
C.A∪B={0,+∞} D.(CRA)∩B={-2,-1}
(2)若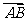 =(2,4),
=(2,4),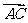 =(1,3),则
=(1,3),则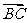 =
=
A.(1,1) B.(-1,-1) C.(3,7) D.(-3,-7)
(3)已知m,n是两条不同直线,α,β,Υ是三个不同平面.下列命题中正确的是
A.若α⊥Υ,β∥Υ,则α∥β B.若m⊥α,n⊥α,则m∥n
C.若m∥α,n∥α,则m∥n D.若m∥α,m∥β,则a∥β
(4)a<0是方程ax2+1=0有一个负数根的
A.必要不充分条件 B.充分必要条件
C.充分不必要条件 D.既不充分也不必要条件
(5)在三角形ABC中,AB=5,AC=3,BC=7,则∠BAC大小为
A.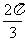 B.
B. 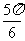 C.
C.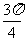 D.
D.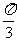
(6) 函数f(x)=(-1)2+1(x≤0)的反函数为
A.f--1(x)=1-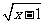
 (x≥1) B. f--2(x)=1+
(x≥1) B. f--2(x)=1+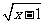 (x≥1)
(x≥1)
C.f--1(x)=1-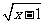 (x≥2) D. f--1(x)=1+
(x≥2) D. f--1(x)=1+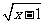 (x≥2)
(x≥2)
(7)设(1+x)8=a0+a1x+…+a8x8,则a0,a1, …a8中奇数的个数为 A.2 B.3 C.4 D.5
(8)函数y=sin(2x+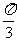 )图像的对称轴方程可能是
)图像的对称轴方程可能是
A.x=-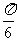 B.x=-
B.x=-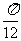 C.x=
C.x=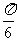 D.x=
D.x=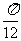
(9)设函数f(x)=2x+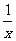 -1(x<0),则f(x)
-1(x<0),则f(x)
A.有最大值 B.有最小值 C.是增函数 D.是减函数
(10)若过A(4,0)的直线l与曲线(x-2)2+y2=1有公共点,则直线l的斜率的取值范围为
A.(-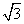 ,
,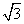 ) B.[-
) B.[-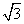 ,
,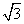 ] C.(-
] C.(-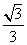 ,
,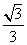 ) D.[-
) D.[-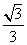 ,
,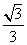 ]
]
(11)若A为不等式组  表示的平面区域,则当a从-2连续变化到1时,动直线x+y=a扫过A中的那部分区域的面积为
表示的平面区域,则当a从-2连续变化到1时,动直线x+y=a扫过A中的那部分区域的面积为
A.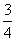 B.1
C.
B.1
C.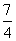 D.2
D.2
12.12名同学合影,站成了前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,其他人的相对顺序不变,则不同调整方法的种数为
A.C38A66 B.C23A23 C.C28A26 D.C28A25
第Ⅱ卷(非选择题 共90分)
请用0.5毫米黑色笔迹签字在答题卡上作答,在试题卷上答题无效.
22.(本小题满分14分)
已知曲线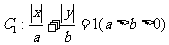 所围成的封闭图形的面积为
所围成的封闭图形的面积为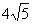 ,曲线
,曲线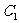 的内
的内
切圆半径为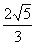 .记
.记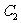 为以曲线
为以曲线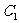 与坐标轴的交点为顶点的椭圆。
与坐标轴的交点为顶点的椭圆。
(I)求椭圆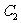 的标准方程,
的标准方程,
(Ⅱ)设AB是过椭圆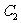 中心的任意弦,
中心的任意弦,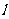 是线段AB的垂直平分线。M是
是线段AB的垂直平分线。M是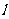 上异于椭圆
上异于椭圆
中心的点。
(1)若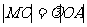 (
(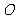 为坐标原点),当点A在椭圆
为坐标原点),当点A在椭圆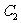 上运动时,求点M的轨迹方
上运动时,求点M的轨迹方
程;
(2)若M是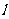 与椭圆
与椭圆 的交点,求△AMB的面积的最小值。
的交点,求△AMB的面积的最小值。
21.(本小题满分12分)
设函数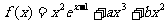 ,已知
,已知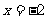 和
和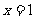 为
为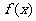 的极值点。
的极值点。
(I)求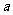 和
和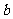 的值,
的值,
(Ⅱ)讨论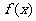 的单调性;
的单调性;
(Ⅲ)设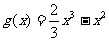 ,试比较
,试比较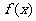 与
与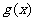 的大小。
的大小。
20.(本小题满分12分)
将数列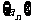 中的所有项按每一行比上一行多一项的规则排成如下数表:
中的所有项按每一行比上一行多一项的规则排成如下数表:

记表中的第一列数a1,a2,,a4,a7,…构成的数列为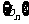 ,b1=a1=1.
,b1=a1=1.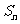 为数列的
为数列的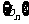
前n项和, 且满足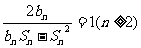 .
.
(I)证明数列 成等差数列, 并求数列
成等差数列, 并求数列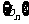 的通项公式;
的通项公式;
(II)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同个正数,当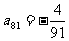 时,求上表中第
时,求上表中第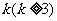 行所有项的和
行所有项的和
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com