
9.从5名男生和5名女生中选3人组队参加某集体项目的比赛,其中至少有一名女生入选的组队方案数为
A.100 B.110 C.120 D.180
8. 函数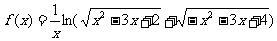 的定义域为
的定义域为
A.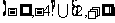 B.
B. 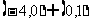
C.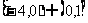 D.
D.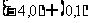
7.将函数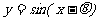 的图象F向右平移
的图象F向右平移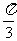 个单位长度得到图象F′,若F′的一条对称轴是直线
个单位长度得到图象F′,若F′的一条对称轴是直线 ,则
,则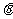 的一个可能取值是
的一个可能取值是
A.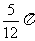 B.
B.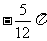 C.
C.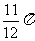 D.
D. 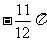
6.已知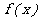 在R上是奇函数,且
在R上是奇函数,且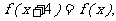 当
当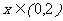 时,
时,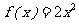 ,则
,则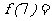
A.-2 B.2 C.-98 D.98
5.在平面直角坐标系x o y中,满足不等式组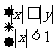 的点(x,y)的集合用阴影表示为下列图中的
的点(x,y)的集合用阴影表示为下列图中的

4.用与球心距离为1的平面去截球,所得的截面面积为 ,则球的体积为
,则球的体积为
A.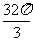 B.
B.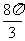 C.
C.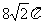 D.
D. 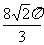
3.若集合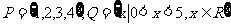 ,则
,则
A.“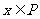 ”是“
”是“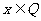 ”的充分条件但不是必要条件
”的充分条件但不是必要条件
B.“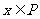 ”是“
”是“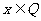 ”的必要条件但不是充分条件
”的必要条件但不是充分条件
C.“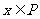 ”是“
”是“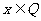 ”的充要条件
”的充要条件
D.“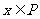 ”既不是“
”既不是“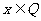 ”的充分条件也不是“
”的充分条件也不是“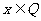 ”的必要条件
”的必要条件
2.  的展开式中常数项是
的展开式中常数项是
A.210
B.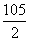 C.
C.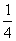 D.-105
D.-105
1.设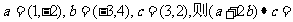
A. (-15, 12) B.0 C.-3 D.-11
(18)(本题14分)已知数列{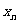 }的首项是x1=3,通项
}的首项是x1=3,通项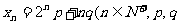 为常数),且
为常数),且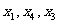 成等差数列。求:
成等差数列。求:
(Ⅰ)p,q的值;
(Ⅱ)数列{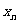 }前n项和
}前n项和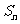 的公式。
的公式。
(19)(本题14分)一个袋中装有大小相同的黑球、白球和红球,已知袋中共有10个球,从中任意摸出1个球,得到黑球的概率是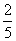 ;从中任意摸出2个球,至少得到1个白球的概率是
;从中任意摸出2个球,至少得到1个白球的概率是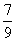 .求:
.求:
(Ⅰ)从中任意摸出2个球,得到的数是黑球的概率;
(Ⅱ)袋中白球的个数。
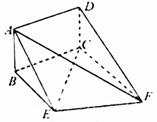
(20)(本题14分)如图,矩形ABCD和梯形BEFC所在平面互相垂直
BE∥CF ,∠BCF=∠CEF=90°,AD=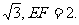
(Ⅰ)求证:AE∥平面DCF;
(Ⅱ)当AB的长为何值时,二面角A-EF-C的大小为60°?
(21)(本题15分)已知a是实数,函数f(x)=x2(x-a).
(Ⅰ)若f1(1)=3,求a的值及曲线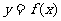 在点
在点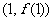 处的切线方程;
处的切线方程;
(Ⅱ)求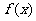 在区间[0,2]上的最大值。
在区间[0,2]上的最大值。
(22)(本题15分)已知曲线C是到点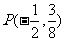 和到直线
和到直线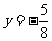 距离相等的点的轨迹,l是过点Q(-1,0)的直线,M是C上(不在l上)的动点;A、B在l上,
距离相等的点的轨迹,l是过点Q(-1,0)的直线,M是C上(不在l上)的动点;A、B在l上,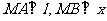 轴(如图)。
轴(如图)。
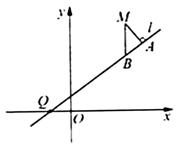
(Ⅰ)求曲线C的方程;
(Ⅱ)求出直线l的方程,使得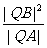 为常数。
为常数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com