20．(本小题满分13分)

若A、B是抛物线y²=4x上的不同两点，弦AB(不平行于y轴)的垂直平分线与x轴相交于点P，则称弦AB是点P的一条“相关弦”．已知当x>2时，点P(x,0)存在无穷多条“相关弦”．给定x₀>2．

(I)证明：点P(x₀,0)的所有“相关弦”的中点的横坐标相同；

(II)试问：点P(x₀,0)的“相关弦”的弦长中是否存在最大值？若存在，求其最大值(用x₀表示)：若不存在，请说明理由．

19．(本小题满分13分)

在一个特定时段内，以点E为中心的7海里以内海域被设为警戒水域．点E正北55海里处有一个雷达观测站A．某时刻测得一艘匀速直线行驶的船只位于点A北偏东且与点A相距40海里的位置B，经过40分钟又测得该船已行驶到点A北偏东+(其中sin=，)且与点A相距10海里的位置C．

(I)求该船的行驶速度(单位：海里/时);

(II)若该船不改变航行方向继续行驶．判断它是否会进入警戒水域，并说明理由．

18．(本小题满分12分)

数列

　 (Ⅰ)求并求数列的通项公式；

　 (Ⅱ)设证明：当

17．(本小题满分12分)

如图所示，四棱锥P-ABCD的底面ABCD是边长为1的菱形，∠BCD＝60°，E是CD的中点，PA⊥底面ABCD，PA＝2．

　 (Ⅰ)证明：平面PBE⊥平面PAB;

(Ⅱ)求平面PAD和平面PBE所成二面角(锐角)的大小．

16．(本小题满分12分)

甲、乙、丙三人参加了一家公司的招聘面试，面试合格者可正式签约，甲表示只要面试合格就签约．乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约．设每人面试合格的概率都是，且面试是否合格互不影响．求：

(Ⅰ)至少有1人面试合格的概率;

(Ⅱ)签约人数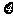的分布列和数学期望．

15．对有n(n≥4)个元素的总体{1,2,3,…,n}进行抽样，先将总体分成两个子总体

{1,2,…，m}和{m+1、m+2,…，n}(m是给定的正整数，且2≤m≤n-2),再从每个子总体中各随机抽取2个元素组成样本，用P_ij表示元素i和j同时出现在样本中的概率，则P_ij=

　　　　　 ;所有P_ij(1≤i＜j≤的和等于 　　　　　　．

14．已知函数f(x)＝

(1)若a＞1,则f(x)的定义域是　　　　　 ;

(2)若f(x)在区间上是减函数，则实数a的取值范围是　　　　　 ．

13．设函数y=f(x)存在反函数y=f^－1(x),且函数y=x-f(x)的图象过点(1,2)．

则函数的图象一定过点　　 　　　．

12．已知椭圆(a＞b＞0)的右焦点为F, 右准线为l, 离心率e=过顶点A(0,b)作AM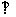l, 垂足为M，则直线FM的斜率等于　　　　　 ．

11．　　　　　　 ．