
(1)已知全集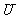 =R,集合A=
=R,集合A=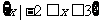 ,B=
,B=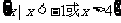 ,那么集合A∩(
,那么集合A∩(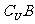 )等于
)等于
A.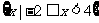 B.
B.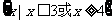
C.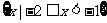 D.
D.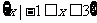
(2)若a=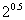 ,b=
,b=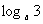 ,c=
,c=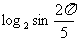 ,则
,则
A.a>b>c B.b>a>c
C.c>a>b D.b>c>a
(3)“函数f(x)(x∈R)存在反函数”是“函数f(x)在R上为增函数”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.即不充分也不必要条件
(4)若点P到直线x=-1的距离比它到点(2,0)的距离小1,则点P的轨迹为
A.圆 B.椭圆 C.双曲线 D.抛物线
(5)若实数x,y满足 则
则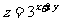 的最小值是
的最小值是
A.0 B.1 C. D.9
D.9
(6)已知数列{an}对任意的p,q∈Nm满足ap+q=ap+aq,且aP=-6,那么ap+q等于
A.-165 B.-33 C.-30 D.-21
(7)过直线y=x上的一点作圆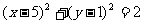 的两条切线
的两条切线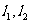 ,当直线
,当直线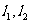 关于y=x对称时,它们之间的夹角为
关于y=x对称时,它们之间的夹角为
A.30° B.45° C.60° D.90°
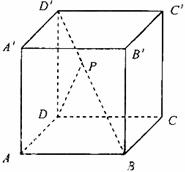
(8)如图,动点P在正方体ABCD-A1B1C1D1的对角线BD1上,过点P作垂直于平面BB1D1D的直线,与正方体面相交于M、N,设BP=x, MN=y,则函数y=f(x)的图象大致是
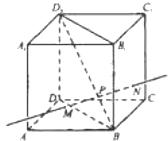
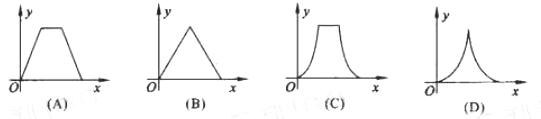
第Ⅱ卷(选择题 共40分)
24.(本小题满分10分)选修4-5:不等式选讲
已知函数f(x)=|x-8|-|x-4|.
(Ⅰ)作出函数y=f(x)的图像:
(Ⅱ)解不等式|x-8|-|x-4|>2.
23.(本小题满分10分)选修4-4;坐标系与参数方程
已知曲线C1: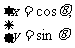 (
(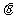 为参数),曲线C2:
为参数),曲线C2: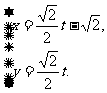 (t为参数).
(t为参数).
(Ⅰ)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(Ⅱ)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线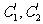 .写出
.写出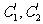 的参数方程.
的参数方程. 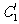 与
与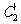 公共点的个数和C
公共点的个数和C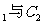 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.
22.(本小题满分10分)选修4-1:几何证明选讲
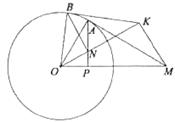
如图,过圆O外一点M作它的一条切线,切点为A,过A点作直线AP垂直直线OM,垂足为P。
(Ⅰ)证明: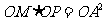
(Ⅱ)N为线段AP上一点,直线NB垂直直线ON,且交圆O于B点,过B点的切线交直线ON于K。证明: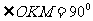
21.(本小题满分12分)
设函数f(x)=ax+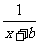 (a, b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程为y=3.
(a, b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程为y=3.
(Ⅰ)求f(x)的解析式:
(Ⅱ)证明:函数y=f(x)的图像是一个中心对称图形,并求其对称中心;
(Ⅲ)证明:曲线y=f(x)上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值,并求出此定值.
请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分。做答时,用2B铅笔在答题卡上把所选题目对应的题号涂黑。
20.(本小题满分12分)
在直角坐标系xOy中,椭圆C1: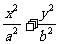 =1(a>b>0)的左、右焦点分别为F1、F2、F2也是抛物线C2: y2=4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|=
=1(a>b>0)的左、右焦点分别为F1、F2、F2也是抛物线C2: y2=4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|=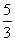 .
.
(Ⅰ)求C1的方程;
(Ⅱ)平面上的点N满足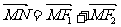 ,直线l∥MN,且与C1交于A、B两点,若
,直线l∥MN,且与C1交于A、B两点,若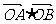 =0,求直线l的方程.
=0,求直线l的方程.
19.(本小题满分12分)
A、B两个投资项目的利润率分别为随机变量X1和X2.根据市场分析,X1,X2的分布列分别为
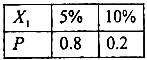
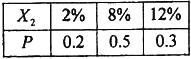
(Ⅰ)在A、B两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求方差DY1,DY2;
(Ⅱ)将x(0≤x≤100)万元投资A项目,100-x万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得到利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.(注:D(aX+b)=a2Dx)
18.(本小题满分12分)
如图,已知点P在正方体ABCD- 的对角线
的对角线 上,
上, .
.
(Ⅰ)求DP与 所成角的大小;
所成角的大小;
(Ⅱ)求DP与平面 所成角的大小.
所成角的大小.
17.(本小题满分12分)
已知{an}是一个等差数列,且a2=1,a5= -5.
(Ⅰ)求{an}的通项an;
(Ⅱ)求{an}前n项和Sn的最大值.
16.从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),结果如下:
甲品种:271 273 280 285 285 287 292 294 295 301 303 303 307
308 310 314 319 323 325 325 328 331 334 337 352
乙品种:284 292 295 304 306 307 312 313 315 315 316 318 318
320 322 322 324 327 329 331 333 336 337 343 356
由以上数据设计了如下茎叶图
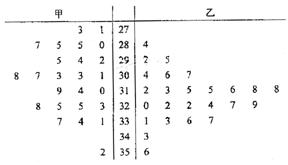
根据以上茎叶图,对甲、乙两品种棉花的纤维长度作比较,写出两个统计结论:
① ;
② .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com