
5.若向量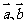 满足
满足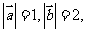 且
且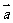 与
与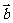 的夹角为
的夹角为 ,则
,则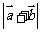 = .
= .
4.若函数f(x)的反函数为f -1(x)=x2(x>0),则f(4)= .
3.若复数z满足z=i(2-z) (i是虚数单位),则z= .
2.若集合A={x|x≤2}、B={x|x≥a}满足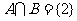 ,则实数a=
.
,则实数a=
.
1.不等式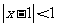 的解集是 .
的解集是 .
(15)(本小题共13分)
已知函数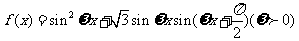 的最小正周期为π.
的最小正周期为π.
(Ⅰ)求ω的值;
(Ⅱ)求函数f(x)在区间[0,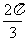 ]上的取值范围.
]上的取值范围.
(16)(本小题共14分)
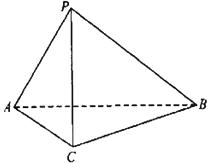
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
(Ⅰ)求证:PC⊥AB;
(Ⅱ)求二面角B-AP-C的大小.
(17)(本小题共13分)
已知函数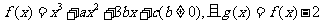 是奇函数.
是奇函数.
(Ⅰ)求a,c的值;
(Ⅱ)求函数f(x)的单调区间.
(18)(本小题共13分)
甲、乙等五名奥运志愿者被随机地分到A,B,C,D四个不同的岗位服务,每个岗位至少有一名志愿者.
(Ⅰ)求甲、乙两人同时参加A岗位服务的概率;
(Ⅱ)求甲、乙两人不在同一个岗位服务的概率.
(19)(本小题共14分)
已知△ABC的顶点A,B在椭圆 上,C在直线l:y=x+2上,且AB∥l.
上,C在直线l:y=x+2上,且AB∥l.
(Ⅰ)当AB边通过坐标原点O时,求AB的长及△ABC的面积;
(Ⅱ)当∠ABC=90°,且斜边AC的长最大时,求AB所在直线的方程.
(20)(本小题共13分)
数列{an}满足 是常数。
是常数。
(Ⅰ)当a2=-1时,求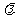 及a3的值;
及a3的值;
(Ⅱ)数列{an}是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由;
(Ⅲ)求 的取值范围,使得存在正整数m,当n>m时总有an<0.
的取值范围,使得存在正整数m,当n>m时总有an<0.
(9)若角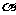 的终边经过点P(1,-2),则tan 2
的终边经过点P(1,-2),则tan 2 的值为 .
的值为 .
(10)不等式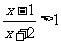 的解集是 .
的解集是 .
(11)已知向量a与b的夹角为120°,且|a|=|b|=4,那么a·b的值为 .
(12)若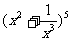
 展开式的各项数之和为
; 各项系数之和为 .(用数字作答)
展开式的各项数之和为
; 各项系数之和为 .(用数字作答)
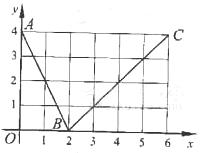
(13)如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))= ; 函数f(x)在x=1处的导数f′(1)= .
(14)已知函数f(x)=x2-cos x,对于[-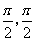 ]上的任意x1,x2,有如下条件:
]上的任意x1,x2,有如下条件:
① x1>x2; ②x21>x22; ③|x1|>x2.
其中能使f(x1)> f(x2)恒成立的条件序号是 .
(1)若集合A={x|-2≤x≤3} , B={x|x<-1或x>4},则集合A∩B等于
A.{x|x≤3或x>4} B.{x|-1<x≤3}
C.{x|3≤x<4} D.{x|-2≤x<-1}
(2)若a=log3π,b=log76,c=log20.8,则
A.a>b>c B.b>a>c
C.c>a>b D.b>c>a
(3)“双曲线的方程为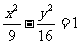 ”是“双曲线的准线方程为x=
”是“双曲线的准线方程为x=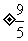 ”的
”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.即不充分也不必要条件
(4)已知△ABC中,a=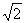 ,b=
,b=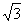 ,B=60°,那么角A等于
,B=60°,那么角A等于
A.135° B.90° C.45° D.30°
(5)函数f(x)=(x-1)2+1(x<1)的反函数为
A.f--1(x)=1+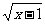 (x>1) B.f--1(x)=1-
(x>1) B.f--1(x)=1-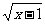 (x>1)
(x>1)
C.f--1(x)=1+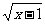 (x≥1) D.f--1(x)=1-
(x≥1) D.f--1(x)=1-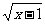 (x≥1)
(x≥1)
(6)若实数x,y满足 ,则z=x+2y的最小值是
,则z=x+2y的最小值是
A.0 B.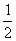 C.1 D.2
C.1 D.2
(7)已知等差数列{an}中,a2=6,a5=15.若bn=a2n,则数列{bn}的前5项和等于
A.30 B.45 C.90 D.186
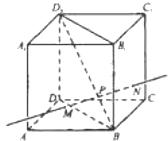
(8)如图,动点P在正方体ABCD-A1B1C1D1的对角线BD1上,过点P作垂直平面BB1D1D的直线,与正方体表面相交于M、N.设BP=x,MN=y,则函数y=f(x)的图象大致是
第Ⅱ卷(共110分)
(15)(本小题共13分)
已知函数f(x)=sin2ωx+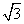 sinωxsin(ωx+
sinωxsin(ωx+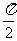 )(ω>0)的最小正周期为π.
)(ω>0)的最小正周期为π.
(Ⅰ)求ω的值;
(Ⅱ)求函数f(x)在区间[0,
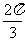 ]上的取值范围.
]上的取值范围.
(16)(本小题共14分)
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
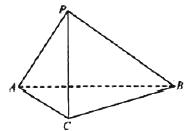
(Ⅰ)求证:PC⊥A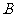 ;
;
(Ⅱ)求二面角B-AP-C的大小;
(Ⅲ)求点C到平面APB的距离.
(17)(本小题共13分)
甲、乙等五名奥运志愿者被随机地分到A,B,C,D四个不同的岗位服务,每上岗位至少有一名志愿者.
(Ⅰ)求甲、乙两人同时参加A岗位服务的概率;
(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;
(Ⅲ)设随机变量ξ为这五名志愿者中参加A岗位服务的人数,求ξ的分布列.
(18)(本小题共13分)
已知函数f(x)=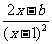 ,求导函数
,求导函数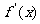 ,并确定f(x)的单调区间.
,并确定f(x)的单调区间.
(19)(本小题共14分)
已知菱形ABCD的顶点A,C在椭圆x2+3y2=4上,对角线BD所在直线的斜率为l.
(Ⅰ)当直线BD过点(0,1)时,求直线AC的方程;
(Ⅱ)当∠ABC=60°,求菱形ABCD面积的最大值.
(20)(本小题共13分)
对于每项均是正整数的数列A:a1,a2,…,an,定义变换T1,T1将数列A变换成数列T1A.:n,a1-1,a2-1,…,an-1.
对于每项均是非负整数的数列B:b1,b2, …,bm,定义变换T2,T2将数列B各项从大到小排列,然后去掉所有为零的项,得到数列T2(B):又定义
S(B)=2(b1+2b2+…+mbm)+b21+b22+…+b2m.
设A0是每项均为正整数的有穷数列,令Ak+1=T2(T1(Ak))(k=0,1,2, …)
(Ⅰ)如果数列A0为5,3,2,写出数列A1,A2;
(Ⅱ)对于每项均是正整数的有穷数列A,证明S(T1A.)=SA.;
(Ⅲ)证明:对于任意给定的每项均为正整数的有穷数列A0,存在正整数K,当k≥K时,S(Ak+1)=S(Ak).
(9)已知(a-i)2=2i,其中是虚数单位,那么实数a= 。
(10)已知向量a与b的夹角为120°,且|a|=|b|=4,那么b·(2a+b)的值为 。
(11)若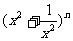
 展开式的各项数之和为32,则n= ,其展开式中的常数项为
展开式的各项数之和为32,则n= ,其展开式中的常数项为
。(用数字作答)
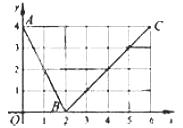
(12)如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))= ;
=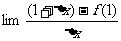 。(用数字作答)
。(用数字作答)
(13)已知函数f(x)=x2-cos x, 对于[-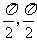 ]上的任意x1,x2,有如下条件:
]上的任意x1,x2,有如下条件:
① x1>x2; ②x21>x22; ③|x1|>x2.
其中能使f(x1)> f(x2)恒成立的条件序是 .
(14)某校数学课外小组在坐标纸上,为学校的一块空地设计植树方案如下:第k棵树种植在点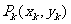 处,其中x1=1,y1=1,当k≥2时,
处,其中x1=1,y1=1,当k≥2时,
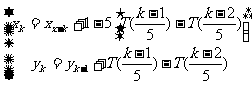
TA.表示非负实数a的整数部分,例如T(2,6)=2,T(0,2)=0。按此方案:第6棵树种植点的坐标应为 ;第2008棵树种植点的坐标应为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com