4．函数的图像关于

A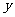．轴对称　 　　　　　　　　　　　　　　　　　　　　　　　　 B．直线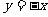对称　

C． 坐标原点对称　 　　　　　　　　　　　　　　　　　　　 D．直线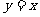对称

3．原点到直线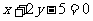的距离为

A．1　 　　　　　　　　　　　　 B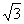．　 　　　　　　　　　　 C．2　 　　　　　　　　　　　 D．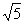

2．设集合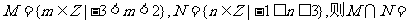

A．{0，1}　 　　　　　　　 B．{-1，0，1}　 　　　　　　　 C．{0，1，2}　 　　　　 D．{-1，0，1，2}

1．若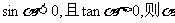是

A．第一象限　 　　　　　　 B．第二象限　 　　　　　　 C．第三象限　 　　　　　　 D．第四象限　

21.(本题满分18分)本题共有3个小题，第1小题满分3分，第2小题满分7分，第3小题满分8分。

已知以a₁为首项的数列{a_n}满足:a_n+1=.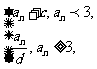

(1)当a₁=1,c=1,d=3时求数列{a _n}的通项公式；

(2)当0＜a₁＜1，c=1,d=3时，试用a₁表示数列{a_n}前100项的和S₁₀₀；

(3)当0＜a₂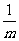＜(m是正整数)，c=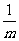，正整数d3m时，求证：数列a₂-，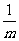

a_3m+2-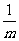,a_6m+2-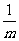,a_9m+2-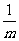成等比数列当且仅当d=3m.

20.(本题满分16分)本题共有3个小题，第1小题满分3分，第2小题满分5分，第3小题满分8分。

设P(a,b)(b≠0)是平面直角坐标系xOy中的点，l是经过原点与点(1，b)的直线，记Q是直线l与抛物线x²=2py(p≠0)的异于原点的交点.

(1)已知a=1,b=2,p=2.求点Q的坐标；

(2)已知点P(a,b)，(ab≠0)在椭圆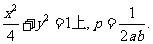求证：点Q落在双曲线=1上；

(3)已知动点P(a,b)满足ab≠0，p=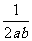，若点Q始终落在一条关于x轴对称的抛物线上，试问动点P的轨迹落在哪种二次曲线上，并说明理由.

19.(本题满分16分)本题共有2个小题，第1小题满分8分，第2小题满分8分.

已知函数f(x)=.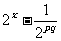

(1)　　 若f(x)＝2，求x的值；

(2)　　 若2^tf(2t)+mf(t)≥0对于t∈［1，2］恒成立，求实数m的取值范围.

18.(本题满分15分)本题共有2个小题，第1个题满分5分，第2小题满分10分.

已知函数f(x)=sin2x,g(x)=cos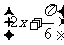,直线x=t(t∈R)与函数f(x)、g(x)的图像分别交于M、N两点.

(1)　　 当t=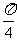时，求｜MN｜的值；

(2)　　 求｜MN｜在t∈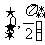时的最大值.

17.(本题满分13分)

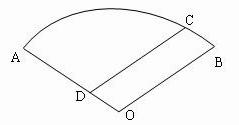
如图，某住宅小区的平面图呈圆心角为120°的扇形AOB.小区的两个出入口设置在点A及点C处，且小区里有一条平等于BO的小路CD.已知某人从C沿CD走到D用了10分钟，从D沿DA走到A用了6分钟.若此人步行的速度为每分钟50米，求该扇形的半径OA的长(精确到1米)

16.(本题满分12分)

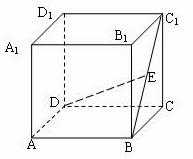
如图，在棱长为2的正方体ABCD-A₁B₁C₁D₁中，E是BC₁的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).