
A.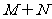 B.
B.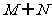 C.
C.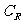 (
(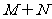 )
D.
)
D.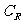 (
(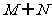 )
)
(2)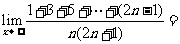
A.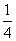 B.
B.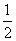 C.1
D.2
C.1
D.2
(3)圆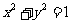 与直线
与直线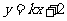 没有公共点的充要条件是
没有公共点的充要条件是
A.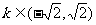 B.
B.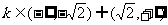
C.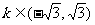 D.
D.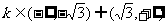
(4)复数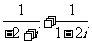 的虚部是
的虚部是
A.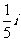 B.
B. C.
C.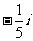 D.
D.
(5)已知O、A、B是平面上的三个点,直线AB上有一点C,满足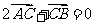 ,则
,则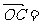
A.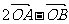 B.
B.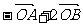 C.
C. D.
D.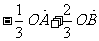
(6)设P为曲线C: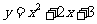 上的点,且曲线C在点P处切线倾斜角的取值范围为[0,
上的点,且曲线C在点P处切线倾斜角的取值范围为[0,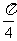 ],则点P横坐标的取值范围为
],则点P横坐标的取值范围为
A.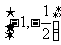 B.
B.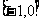 C.
C.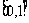 D.
D.
(7)4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数学之和为奇数的概率为
A.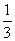 B.
B.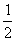 C.
C.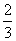 D.
D.
(8)将函数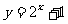 的图象按向量
的图象按向量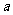 平移得到函数
平移得到函数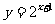 的图像,则
的图像,则
A.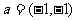 B.
B.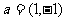 C.
C.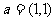 D.
D.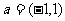
(9)一生产过程有4道工序,每道工序需要安排一人照看,现从甲、乙、丙等6名工人中安排4人分别照看一道工序,第一道工序只能从甲、乙两工人中安排1人,第四道工序只能从甲、丙两工人中安排1人,则不同的安排方案共有
A.24种 B.36种 C.48种 D.72种
(10)已知点P是抛物线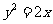 上的一个动点,则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为
上的一个动点,则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为
A. B.3 C.
B.3 C. D.
D.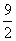
(11)在正方体ABCD-A1B1C1D1中,E、F分别为棱AA1,CC1的中点,则在空间中与三条直线A1D1、EF、CD都相交的直线
A.不存在 B.有且只有两条 C.有且只有三条 D.有无数条
(12)设f(x)是连续的偶函数,且当x>0时f(x)是单调函数,则满足f(x)=f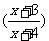 的所有x之和为
的所有x之和为
A.-3 B.3 C.-8 D.8
第Ⅱ卷(选择题共60分)
23.(本小题满分10分)选修4-4;坐标系与参数方程
已知曲线C1: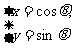 (
(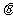 为参数),曲线C2:
为参数),曲线C2: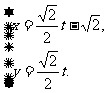 (t为参数).
(t为参数).
(Ⅰ)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(Ⅱ)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线 .写出
.写出 的参数方程.
的参数方程. 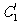 与
与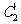 公共点的个数和C
公共点的个数和C 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.
22.(本小题满分10分)选修4-1:几何证明选讲
如图,过圆O外一点M作它的一条切线,切点为A,过A点作直线AP垂直直线OM,垂足为P。
(Ⅰ)证明: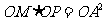
(Ⅱ)N为线段AP上一点,直线NB垂直直线ON,且交圆O于B点,过B点的切线交直线ON于K。证明: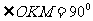

21.(本小题满分12分)
设函数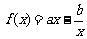 ,曲线
,曲线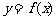 在点(2,
在点(2,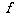 (2))处的切线方程为
(2))处的切线方程为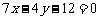
(Ⅰ)求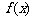 的解析式:
的解析式:
(Ⅱ)证明:曲线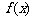 上任一点处的切线与直线
上任一点处的切线与直线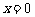 和直线
和直线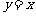 所围成的三角形面积为一值,并求此定值。
所围成的三角形面积为一值,并求此定值。
请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目对应的题号涂黑。
20.(本小题满分12分)
已知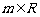 ,直线
,直线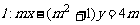 和圆C:
和圆C:
(Ⅰ)求直线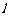 斜率的取值范围;
斜率的取值范围;
(Ⅱ)直线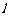 能否将圆C分割成弧长的比值为
能否将圆C分割成弧长的比值为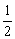 的两段圆弧?为什么?
的两段圆弧?为什么?
19.(本小题满分12分)
为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查,6人得分情况如下:
5,6,7,8,9,10
把这6名学生的得分看成一个总体。
(Ⅰ)求该总体的平均数;
(Ⅱ)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本,求该样本平均数与总体平均数之差的绝对值不超过0.5的概率。
18.(本小题满分12分)
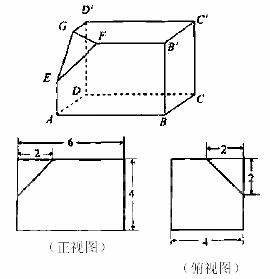
如下的三个图中,上面的一个长方体截去一个角所得多面体的直观图,正视图和侧视图在下面画出(单位:cm)
(Ⅰ)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(Ⅱ)按照给出的尺寸,求该多面体的体积;
(Ⅲ)在所给直观图中连续BC’,证明BC’//面EFG
17.(本小题满分12分)
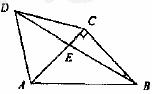
如图△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2
(Ⅰ)求cos∠CBE的值;
(Ⅱ)求AE
16.从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),结果如下:
甲品种:271 273 280 285 285 287 292 294 295 301 303 303 307
308 310 314 319 323 325 325 328 331 334 337 352
乙品种:284 292 295 304 306 307 312 313 315 315 316 318 318
320 322 322 324 327 329 331 333 336 337 343 356
由以上数据设计了如下茎叶图
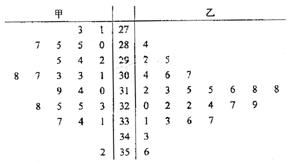
根据以上茎叶图,对甲、乙两品种棉花的纤维长度作比较,写出两个统计结论:
① ;
② .
15.过椭圆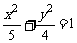 的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为 .
的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com