

5.设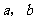 是两条直线,
是两条直线,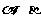 是两个平面,则
是两个平面,则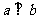 的一个充分条件是( )
的一个充分条件是( )
A.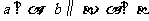 B.
B.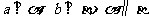
C.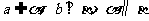 D.
D.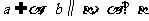
4.若等差数列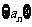 的前5项和
的前5项和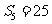 ,且
,且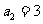 ,则
,则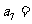 ( )
( )
A.12 B.13 C.14 D.15
3.函数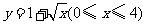 的反函数是( )
的反函数是( )
A.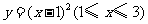 B.
B.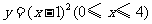
C.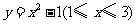 D.
D.
2.设变量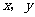 满足约束条件
满足约束条件 则目标函数
则目标函数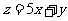 的最大值为( )
的最大值为( )
A.2 B.3 C.4 D.5
1.设集合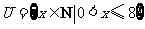 ,
,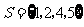 ,
,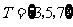 ,则
,则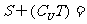 ( )
( )
A. B.
B.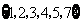 C.
C.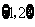 D.
D.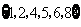
(17)(本小题满分12分)
在△ABC中,内角A,B,C,对边的边长分别是a,b,c.已知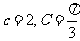 .
.
(Ⅰ)若△ABC的面积等于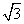 ,求a,b;
,求a,b;
(Ⅱ)若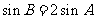 ,求△ABC的面积.
,求△ABC的面积.
(18)(本小题满分12分)
某批发市场对某种商品的周销售量(单位:吨)进行统计,最近100周的统计结果如下表所示:
|
周销售量 |
2 |
3 |
4 |
|
频数 |
20 |
50 |
30 |
(Ⅰ)根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
(Ⅱ)若以上述频率作为概率,且各周的销售量相互独立,求
(i)4周中该种商品至少有一周的销售量为4吨的概率;
(ii)该种商品4周的销售量总和至少为15吨的概率.
(19)(本小题满分12分)
如图,在棱长为1的正方体ABCD-A′B′CD′中,AP=BQ=b(0<b<1),截面PQEF∥A′D,截面PQGH∥AD′.
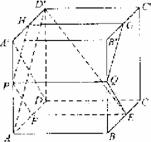
(Ⅰ)证明:平面PQEF和平面PQGH互相垂直;
(Ⅱ)证明:截面PQEF和截面PQGH面积之和是定值,并求出这个值;
(Ⅲ)若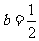 ,求D′E与平面PQEF所成角的正弦值.
,求D′E与平面PQEF所成角的正弦值.
(20)(本小题满分12分)
已知数列{an},{bn}是各项均为正数的等比数列,设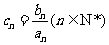 .
.
(Ⅰ)数列{cn}是否为等比数列?证明你的结论;
(Ⅱ)设数列{lnan},{lnbn}的前n项和分别为Sn,Tn.若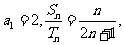 求数列{cn}的前n项和.
求数列{cn}的前n项和.
(21)(本小题满分12分)
在平面直角坐标系xOy中,点P到两点(0,-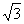 )、(0,
)、(0,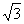 )的距离之和等于4.设点P的轨迹为C.
)的距离之和等于4.设点P的轨迹为C.
(Ⅰ)写出C的方程;
(Ⅱ)设直线y=kx+1与C交于A、B两点.k为何值时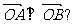 此时|
此时|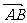 |的值是多少?
|的值是多少?
(22)(本小题满分14分)
设函数f(x)=ax3+bx2-3a2x+1(a、b∈R)在x=x1,x=x2处取得极值,且|x1-x2|=2.
(Ⅰ)若a=1,求b的值,并求f(x)的单调区间;
(Ⅱ)若a>0,求b的取值范围.
(13)函数 的反函数是
.
的反函数是
.
(14)在体积为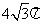 的球的表面上有A、B、C三点,AB=1,BC=
的球的表面上有A、B、C三点,AB=1,BC=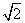 ,A、C两点的球面离为
,A、C两点的球面离为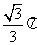 ,则球心到平面ABC的距离为
.
,则球心到平面ABC的距离为
.
(15)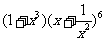 展开式中的常数项为 .
展开式中的常数项为 .
(16)设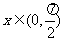 ,则函数
,则函数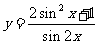 的最小值为
.
的最小值为
.
(1)已知集合M={x|-3<x<1|,N={x|x≤-3},则M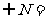 A.
A.
A.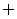 B. {x|x≥-3} C.{x|x≥1} D.{x|x<1|
B. {x|x≥-3} C.{x|x≥1} D.{x|x<1|
(2)若函数y=(x+1)(x-a)为偶函数,则a=
A.-2 B. -1 C.1 D.2
(3)圆x2+y2=1与直线y=kx+2没有公共点的充要条件是
A.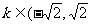 ) B.) k
) B.) k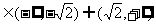
C.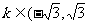 ) D. k
) D. k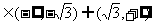
(4)已知0<a<1,x=loga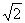 +loga
+loga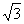 ,y=
,y=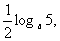 z= loga
z= loga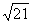 -loga
-loga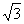 ,则
,则
A.x>y>z B.z>y>x C.y>x>z D.z>x>y
(5)已知四边形ABCD的三个顶点A(0,2),B(-1,-2),C(3,1),且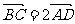 ,则顶点D的坐标为
,则顶点D的坐标为
A.(2,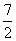 ) B.(2,-
) B.(2,-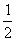 ) C.(3,2) D.(1,3)
) C.(3,2) D.(1,3)
(6)设P为曲线C:y=x2+2x+3上的点,且曲线C在点P处切线倾斜角的取值范围为
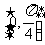 ,则点P横坐标的取值范围为
,则点P横坐标的取值范围为
A. B.[-1,0] C.[0,1] D.
B.[-1,0] C.[0,1] D.
(7)4张卡片上分别写有数字1,2,3,4从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为
A.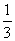 B.
B.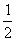 C.
C.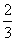 D.
D.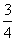
(8)将函数y=2x+1的图象按向量a平移得到函数y=2x+1的图象,则
A.a=(-1,-1) B.a=(1,-1)
C.a=(1,1) D.a=(-1,1)
(9)已知变量x、y满足约束条件 则z=2x+y的最大值为
则z=2x+y的最大值为
A.4 B.2 C.1 D.-4
(10)一生产过程有4道工序,每道工序需要安排一人照看,现从甲、乙、丙等6名工人中安排4人分别照看一道工序,第一道工序只能从甲、乙两工人中安排1人,第四道工序只能从甲、丙两工人安排1人,则不同的安排方案共有
A.24种 B.36种 C.48种 D.72种
(11)已知双曲线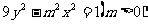 的一个顶点到它的一条渐进线的距离为
的一个顶点到它的一条渐进线的距离为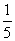 ,则m=
,则m=
A.1 B.2 C.3 D.4
(12)在正方形ABCD-A1B1C1D1中,E、F分为棱AA1CC1的中点,则在空间中与三条直线A1D1、EF、CD都相交的直线
A.不存在 B.有且只有两条 C.有且只有三条 D.有无数条
第Ⅱ卷(非选择题 共90分)
(17)(本小题满分12分)
在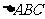 中,内角A,B,C对边的边长分别是a,b,c,已知c=2,C=
中,内角A,B,C对边的边长分别是a,b,c,已知c=2,C=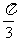 .
.
(Ⅰ)若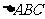 的面积等于
的面积等于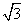 ,求a, b;
,求a, b;
(Ⅱ)若 ,求
,求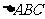 的面积.
的面积.
(18)(本小题满分12分)
某批发市场对某种商品的周销售量(单位:吨)进行统计,最近100周的统计结果如下表所示:

(Ⅰ)根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
(Ⅱ)已知每吨该商品的销售利润为2千元,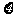 表示该种商品两周销售利润的和(单位:千元).若以上述频率作为概率,且各周的销售量相互独立,求
表示该种商品两周销售利润的和(单位:千元).若以上述频率作为概率,且各周的销售量相互独立,求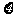 的分布列和数学期望.
的分布列和数学期望.
(19)(本小题满分12分)
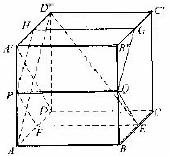
如图,在棱长为1的正方体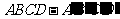 中,AP=BP=b(0<b<1),截面PQEF∥
中,AP=BP=b(0<b<1),截面PQEF∥ ,截面PQGH∥
,截面PQGH∥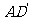 .
.
(Ⅰ)证明:平面PQEF和平面PQGH互相垂直;
(Ⅱ)证明:截面PQEF和截面PQGH面积之和是定值,并求出这个值;
(Ⅲ)若 与平面PQEF所成的角为45°,求
与平面PQEF所成的角为45°,求 与平面PQGH所成角的正弦值.
与平面PQGH所成角的正弦值.
(20)(本小题满分12分)
在直角坐标系xoy中,点P到两点(0,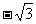 )、(0,
)、(0, )的距离之和等于4,设点P的轨迹为l、直线y=kx+1与C交于A、B两点.
)的距离之和等于4,设点P的轨迹为l、直线y=kx+1与C交于A、B两点.
(Ⅰ)写出C的方程;
(Ⅱ)若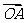
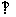
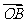 ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有|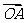 |>|
|>|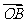 |.
|.
(21)(本小题满分12分)
在数列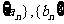 |中,a1=2,
b1=4,且
|中,a1=2,
b1=4,且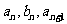 成等差数列,
成等差数列,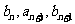 成等比数列(
成等比数列(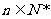 )
)
(Ⅰ)求a2, a3, a4及b2, b3, b4,由此猜测{an},{bn}的通项公式,并证明你的结论;
(Ⅱ)证明: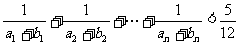 .
.
(22)(本小题满分14分)
设函数f(x)=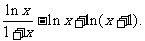
(Ⅰ)求f(x)的单调区间和极值;
(Ⅱ)是否存在实数a,使得关于x的不等式f(x) a的解集为(0,+
a的解集为(0,+ )?若存在,求a的取值范围;若不存在,试说明理由.
)?若存在,求a的取值范围;若不存在,试说明理由.
(13)函数 的反函数是__________.
的反函数是__________.
(14)在体积为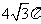 的球的表面上有A、B、C三点,AB=1,BC=
的球的表面上有A、B、C三点,AB=1,BC=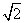 ,A、C两点的球面距离为
,A、C两点的球面距离为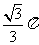 ,则球心到平面ABC的距离为_________.
,则球心到平面ABC的距离为_________.
(15)已知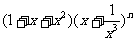 的展开式中没有常数项,
的展开式中没有常数项,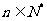 ,且2≤n≤8,则n=______.
,且2≤n≤8,则n=______.
(16)已知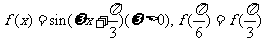 ,且
,且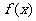 在区间
在区间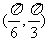 有最小值,无最大值,则
有最小值,无最大值,则 =__________.
=__________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com