2．命题p：不等式；命题q：“A=B”是“sinA=sinB”成立的必要非充分条件，则　　 　　　　　　　　　　　　　　　　 (　　 )

　　　 A．p真q假　　　　　　 B．“p且q”为真　　　　 C．“p或q”为假　　　　　　　　　 D．p假q真

1．设全集U={1，3，5，7}，集合M={1，a－5}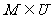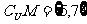，，， 则a的值为

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．2　　　　　　　　　　　　 B．8　　　　　　　　　　　　 C．－2　　　　　　　　　　 D．－8

21．(本小题满分14分)

过x轴上的动点A(a，0)向抛物线y=x²+1引两切线AP、AQ，P、Q为切点.

(1)若切线AP、AQ的斜率分别为k₁，k₂，求证：k₁k₂为定值；

(2)求证：直线PQ过定点；

(3)若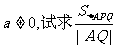的最小值.

20．(本小题满分13分)

设数列{a_n}的前n项和S_n=n²－4n+4.

(1)求数列{a_n}的通项公式；

(2)设各项均不为0的数列{b_n}中，所有满足b_i·b_i+1<0的整数i的个数称为这个数列{b_n}的变号数，令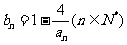，求数列{b_n}的变号数；

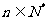(3)试求实数λ的取值范围，使得不等式对一切恒成立.

19．(本小题满分12分)

长沙市某民营化工企业经过近十年打拼，目前净资产已达3千万元. 由于种种原因，影响了企业的进一步发展，企业领导班子决定对企业内部所有环节进行改革. 据市场调查报告显示：在未来五年内，若引进新的技术及设备改造后，企业的生产总量为x千吨，最大限度不能超过4千吨，而每千吨销售可获纯利P(x)与生产总量x的函数关系为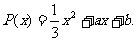 由于该企业的产品市场占有量较大，产量的大小对每千吨产品的纯利润影响较大. 如果企业的生产总量为1千吨时，市场该产品每千吨销售可获纯利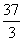万元，如果生产总量达到最大限度值4千吨，此时市场需求趋于饱和状态，每千吨销售只能获纯利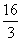万元.企业在人员工资给、产品广告费用及环境污染治理等方面需投入每千吨1万元.

(1)求出常数a，b的值；

(2)求出该企业在未来五年内净资产的总额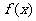(单位：千万元)关于生产总量x(单位：千吨)的函数表达式；

(3)当生产总量x(单位：千吨)取值为多少时，该企业在未来五年内净资产的总额(单位：千万元)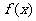取最大值，并求出此最大值.

18．(本小题满分12分)

已知多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，AC=AD=CD=DE=2a，AB=a，F为CD的中点.

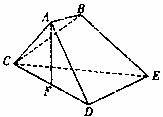
(1)求证：AF⊥平面CDE；

(2)求异面直线AC，BE所成角的余弦值；

(3)求面ACD和面BCE所成锐二面角的大小.

17．(本小题满分12分)

一个盒子装有六张卡片，上面分别写着如下六个定义域为R的函数：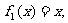

(1)现从盒子中任取两张卡片，将卡片上的函数相加得一个新函数，求所得函数是奇函数的概率；

(2)现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张记有偶函数的卡片则停止抽取，否则继续进行，求抽取次数ξ的分布列和数学期望.

16．(本小题满分12分)

若函数的图象与直线y=m相切，并且切点的横坐标依次成公差为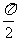的等差数列.

(1)求m的值；

(2)若点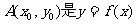图象的对称中心，且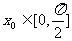，求点A的坐标.

15．已知向量a=(cosθ，sinθ)，b=(3，4)，其中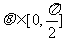，则a·b的最小值为　　　　　 .三、解答题：本大题共6小题，共75分. 解答应写出文字说明、证明过程或演算步骤.

14．某学校对学生的身高进行统计，所有学生的身高近似服从正态分布N(160，25). 已知所有学生中身高在153厘米以下的人数为202人，则该校总人数约为　 　　　人.

()