
4.已知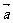 ,
,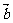 是两个相互垂直的单位向量,而
是两个相互垂直的单位向量,而 ,
,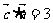 ,
,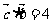 . 则对于任意实数
. 则对于任意实数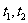 ,
,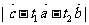 的最小值是
的最小值是
A.5 B.7 C.12 D.13
3.设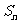 为等差数列
为等差数列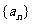 的前n项的和,
的前n项的和,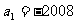 ,
,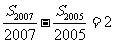 ,则
,则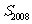 的值为
的值为
A.-2007 B.-2008 C.2007 D.2008
2.已知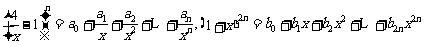 ,
,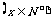 .
.
记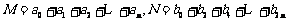 ,则
,则 的值是
的值是
A.2 B.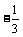 C.0 D.
C.0 D.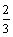
1.设条件p: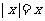 ;条件q:
;条件q: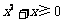 ,那么p是q的什么条件
,那么p是q的什么条件
A.充分非必要条件 B.必要非充分条件
C.充分且必要条件 D.非充分非必要条件
22.本小题满分14分)
设函数 其中实数
其中实数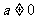 .
.
(Ⅰ)若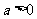 ,求函数
,求函数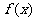 的单调区间;
的单调区间;
(Ⅱ)当函数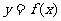 与
与 的图象只有一个公共点且
的图象只有一个公共点且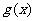 存在最小值时,记
存在最小值时,记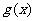 的最小值为
的最小值为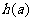 ,求
,求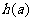 的值域;
的值域;
(Ⅲ)若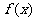 与
与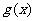 在区间
在区间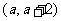 内均为增函数,求
内均为增函数,求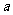 的取值范围.
的取值范围.
21.(本小题满分12分)
已知抛物线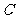 :
: ,直线
,直线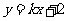 交
交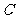 于
于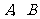 两点,
两点,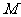 是线段
是线段 的中点,过
的中点,过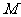 作
作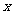 轴的垂线交
轴的垂线交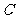 于点
于点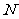 .
.
(Ⅰ)证明:抛物线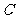 在点
在点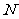 处的切线与
处的切线与 平行;
平行;
(Ⅱ)是否存在实数 使
使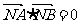 ,若存在,求
,若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
20.(本小题满分12分)
已知数列 的首项
的首项 ,
, ,
,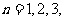 ….
….
(Ⅰ)证明:数列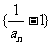 是等比数列;
是等比数列;
(Ⅱ)数列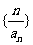 的前
的前 项和
项和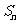 .
.
19.(本小题满分12分)
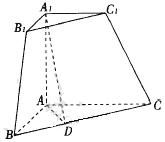
三棱锥被平行于底面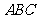 的平面所截得的几何体如图所示,截面为
的平面所截得的几何体如图所示,截面为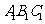 ,
,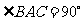 ,
,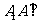 平面
平面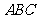 ,
, ,
,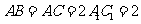 ,
,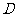 为
为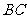 中点.
中点.
(Ⅰ)证明:平面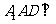 平面
平面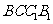 ;
;
(Ⅱ)求二面角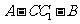 的大小.
的大小.
18.(本小题满分12分)
一个口袋中装有大小相同的2个红球,3个黑球和4个白球,从口袋中一次摸出一个球,摸出的球不再放回.
(Ⅰ)连续摸球2次,求第一次摸出黑球,第二次摸出白球的概率;
(Ⅱ)如果摸出红球,则停止摸球,求摸球次数不超过3次的概率.
17.(本小题满分12分)
已知函数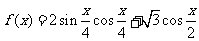 .
.
(Ⅰ)求函数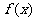 的最小正周期及最值;
的最小正周期及最值;
(Ⅱ)令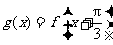 ,判断函数
,判断函数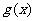 的奇偶性,并说明理由.
的奇偶性,并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com