4．由0，1，2，3这四个数字组成的四位数中，有重复数字的四位数共有　　　　　　　 (　　 )

　　　 A．238个　　　　　　　　　 B．232个　　　　　　　 C．174个　　　　　　　　　 D．168个

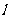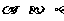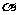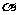3．已知、m、n是两两不重合的直线，是两两不重合的平面，给出下列命题：①若m∥l且m⊥;则l⊥;②若m∥l,且m∥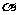,则l∥;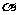

　　　 ③若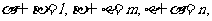则l∥m∥n; ④若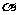l∥,l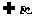,m∥β,m且直线l、m为异面直线，则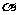∥β，其中真命题的序号为　　　　　　　　　　　　　　　 (　　 )

　　　 A．①②　　　　　　　　　　 B．①③　　　　　　　　　 C．①④　　　　　　　　　　 D．②④

2． 直线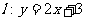被圆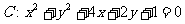所截得弦的长为　　　　　　 (　　 )

　　　 A．1　　　　　　　　　　　　　 B．2　　　　　　　　　　　 C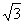．　　　　　　　　　　 D．4

1．(文)已知集合U={1,2,3,4,5,6,7},A={2,4,5,7},B={3,4,5,},则(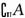)∩B=　　　　　　　 (　　 )

　　　 A．{1,6}　　　　　　　　　 B．{3}　　　　　　　　　 C．{2,3,4,5,7}　　　　　 D．{1,3,4,6,7}

　　　 (理)设a是实数,且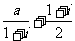是实数(i是虚数单位)，则a＝　　　　　　　　　　　　　　 (　　 )

　　　 A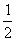．　　　　　　　　　　　 B．1　　　　　　　　　　　 C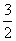．　　　　　　　　　　　 D．2

21．已知函数().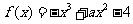

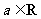　　 (I)若函数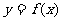的图象在点P(1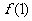，)处的切线的倾斜角为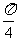，求a；

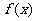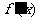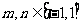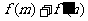　　 (II)设的导函数是.在(I)的条件下，若，求的最小值；

(Ⅲ)若存在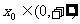，使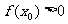，求a的取值范围.

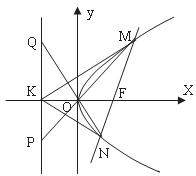
20．(本题满分13分)如图,已知抛物线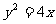的焦点为F，过F的直线交抛物线于M、N两点，其准线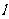与x轴交于K点.

(1)写出抛物线的焦点坐标及准线方程；

(2)求证：KF平分∠MKN；

(3)O为坐标原点，直线MO、NO分别交准线于点P、Q，设直线MN的倾斜角为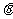，试用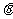表示线段PQ的长度|PQ|，并求|PQ|的最小值.

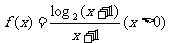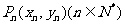19．(本题满分12分)已知曲线上有一点列，点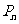在x轴上的射影是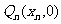，且，.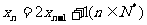

(1)求数列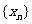的通项公式；

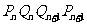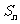(2)设四边形的面积是，求证：。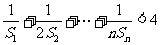

18．如图，直三棱柱A₁B₁C₁-ABC中，C₁C=CB=CA=2，AC⊥CB. D、E分别为棱C₁C、B₁C₁的中点.

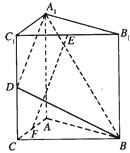
　　 (Ⅰ)求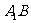与平面A₁C₁CA所成角的大小；

　　 (Ⅱ)求二面角B-A₁D-A的大小；

　　　 (Ⅲ)试在线段AC上确定一点F，使得EF⊥平面A₁BD.

17．(本小题共12分)甲、乙、丙三人组成一组，参加一个闯关游戏团体赛.三人各自独立闯关，其中甲闯关成功的概率为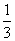，甲、乙都闯关成功的概率为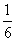，乙、丙都闯关成功的概率为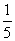.每人闯关成功记2分，三人得分之和记为小组团体总分.

(I)求乙、丙各自闯关成功的概率；

(II)求团体总分为4分的概率；

(III)若团体总分不小于4分，则小组可参加复赛.求该小组参加复赛的概率.

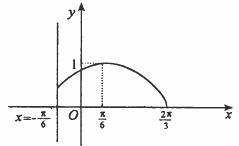
16．已知定义在区间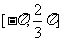上的函数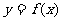的图象关于直线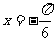对称，当

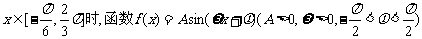的图象如图.

(1)求函数上的表达式；

(2)求方程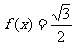的解.