
2.函数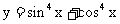 的最小正周期是( )
的最小正周期是( )
A.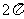 B.
B.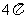 C.
C. 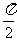 D.
D.
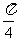
1.已知集合M=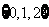 ,N=
,N=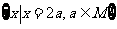 ,则集合
,则集合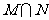 =( )
=( )
A、 B、
B、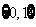 C、
C、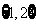 D、
D、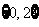
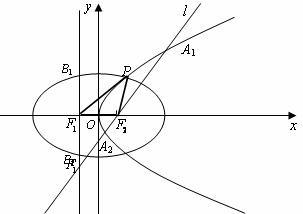
21.(本小题满分14分)如图,设抛物线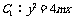
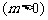 的准线与
的准线与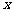 轴交于
轴交于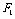 ,焦点为
,焦点为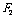 ;以
;以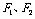 为焦点,离心率
为焦点,离心率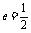 的椭圆
的椭圆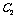 与抛物线
与抛物线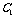 在
在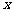 轴上方的一个交点为
轴上方的一个交点为 .
.
(Ⅰ)当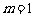 时,求椭圆的方程及其右准线的方程;
时,求椭圆的方程及其右准线的方程;
(Ⅱ)在(Ⅰ)的条件下,经过点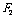 的直线
的直线 与抛物线
与抛物线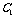 交于
交于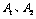 ,如果以线段
,如果以线段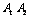 为直径作圆,试判断抛物线
为直径作圆,试判断抛物线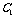 的准线与椭圆
的准线与椭圆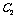 的交点
的交点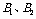 与圆的位置关系;
与圆的位置关系;
(Ⅲ)是否存在实数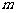 ,使得△
,使得△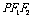 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数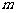 ;若不存在,请说明理由.
;若不存在,请说明理由.
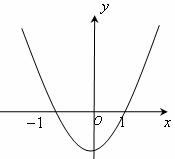
20.(本小题满分13分)设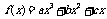 的极小值为
的极小值为 ,其导函数
,其导函数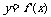 的图像是经过点
的图像是经过点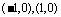 开口向上的抛物线,如图所示.
开口向上的抛物线,如图所示.
(Ⅰ)求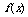 的解析式;
的解析式;
(Ⅱ)若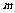

 ,且过点(1,m)可作曲线
,且过点(1,m)可作曲线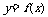 的三条切线,求实数
的三条切线,求实数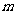 的取值范围.
的取值范围.
19.(本小题满分12分)如图,在直三棱柱ABC-A1B1C1中, .
.
(Ⅰ)若D为AA1中点,求证:平面B1CD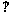 平面B1C1D;
平面B1C1D;
(Ⅱ)若二面角B1-DC-C1的大小为60°,求AD的长.

18.(本小题满分12分)已知Sn是首项为a的等比数列{an}的前n项和,S4、S6、S5成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若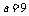 ,
,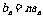 ,数列{bn}的前n项和Tn ,求T10
.
,数列{bn}的前n项和Tn ,求T10
.
17.(本小题满分12分)一批产品成箱包装,每箱6件. 一用户在购买这批产品前先取出2箱,再从取出的每箱中抽取2件检验. 设取出的第一、二箱中二等品分别装有1件、n件,其余均为一等品.
(Ⅰ)若n=2,求取到的4件产品中恰好有2件二等品的概率;
(Ⅱ)若取到的4件产品中含二等品的概率大于0.80,用户拒绝购买,求该批产品能被用户买走的n的值.
16.(本小题满分12分)在锐角三角形ABC中,已知内角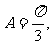 边
边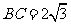 ,设内角B=x,三角形ABC的面积为S.
,设内角B=x,三角形ABC的面积为S.
(Ⅰ)试用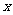 表示AB边的长;
表示AB边的长;
(Ⅱ)求面积S的最大值.
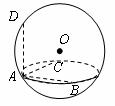
15.如图, 设A、B、C、D为球O上四点,若AB、AC、AD两两互相垂直,且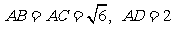 ,则AD两点间的球面距离
.
,则AD两点间的球面距离
.
14.设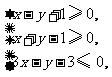 则函数
则函数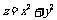 取最小值时,
取最小值时,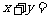 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com