
4.若△ABC的内角A满足球sinA+cosA>0,tanA-sinA<0, 则角A的取值范围是 ( )
A.(0,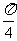 ) B.[0,1] C.(
) B.[0,1] C.(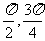 ) D.(
) D.(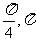 )
)
3.若平面向量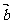 现向量
现向量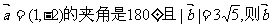 等于 ( )
等于 ( )
A.(-1,2) B.(-3,6) C.(3,-6) D.(-3,6)或(3,-6)
2.函数f(x)=ax3+x+1有极值的充要条件是 ( )
A. B.
B.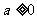 C.
C.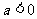 D.
D.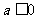
1.设集合P=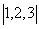 ,集合Q=
,集合Q=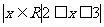 ,那么下列结论正确的是 ( )
,那么下列结论正确的是 ( )
A.P∩Q=Q B.Q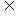 P∩Q C.P∩Q
P∩Q C.P∩Q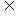 P D.P∩Q=P
P D.P∩Q=P
22.(本题满分14分)
设向量 ,函数
,函数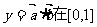 上的最小值最最大值和为
上的最小值最最大值和为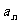 ,又数列
,又数列
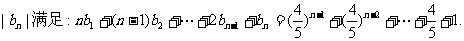
(1)求证: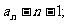
(2)求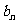 的表达式;
的表达式;
(3)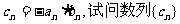 中,是否存在正整数k,使得对于任意的正整数n,都有
中,是否存在正整数k,使得对于任意的正整数n,都有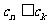 成立?证明你的结论。
成立?证明你的结论。
21.(本小题满分12分)已知函数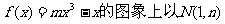 为切点的切线倾斜角为
为切点的切线倾斜角为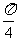 .
.
(1)求m,n的值;
(2)是否存在最小的正整数k,使得不等式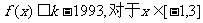 恒成立?若存在,求出最小的正整数k,否则请说明理由。
恒成立?若存在,求出最小的正整数k,否则请说明理由。
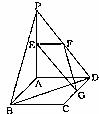
20.(本小题满分12分)如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2;E、F、G分别是线段PA、PD、CD的中点。
(1)求证:PB//平面EFG;
(2)求异面直线:EG与BD所成的角;
(3)在线段CD上是否存在一点Q,使得A到平面EFQ的距离为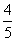 ,若存在,求出CQ的值;若不存在,请说明理由。
,若存在,求出CQ的值;若不存在,请说明理由。
19.(本小题满分12分)
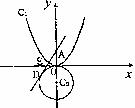
如图,已知抛物线C1:y=x2,与圆C2:x2+(y+1)2=1,过y轴上一点A(0,a),(a>0),作圆C2的切线AD,切点为D(x0,y0).
(1)证明:(a+1)(y0+1)=1;
(2)若切线AD交抛物线C1于E,且E为AD的中点,求点A纵坐标a.
18.(本小题满分12分)
某种仪表批示灯,只有“红灯”“绿灯”,且随机反复出现,每分钟变化一次,每次变化出现“红灯”“绿灯”之一,其中出现“红灯”的概率为p,出现“绿灯”的概率为q,若第1次出现“红灯”,则记ak=1;出现“绿灯”,则记ak=-1,令Sn=a1+a1…+an
(1)当p=q=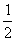 时,记ξ=
时,记ξ=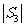 ,求ξ的分布列和数学期望;
,求ξ的分布列和数学期望;
(2)当p=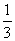 ,q=
,q=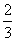 时,求S1=2且S1≥(i=1,2,3,4,)的概率
时,求S1=2且S1≥(i=1,2,3,4,)的概率
17.(本题满分12分)
若函数f(x)=sinx2ax-sinaxcosax(a>0)的图象与直线y=m相切,并且切点的横坐标依次成公差为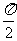 的等差数列
的等差数列
(1)求a和m的值
(2) 若点A(x0,y0)是y=f(x)图像的对称中心,且x0∈[0,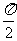 ],求点A的坐标
],求点A的坐标
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com