
1.设集合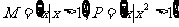 ,则下列关系中正确的是
,则下列关系中正确的是
A.M=P B.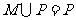 C.
C.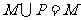 D.
D.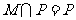
22.(本题满分14分)已知数列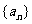 是公比为3的等比数列,数列
是公比为3的等比数列,数列
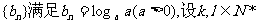 ,
,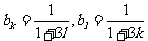 。
。
(1)求证:数列 为等差数列;
为等差数列;
(2)若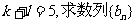 的通项公式;
的通项公式;
(3)若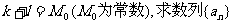 的第几项起,后面的项都满足
的第几项起,后面的项都满足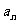 >1。
>1。
21.(本小题满分12分)已知函数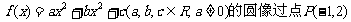 ,且在点P处的切线与直线
,且在点P处的切线与直线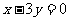 垂直。
垂直。
(1)若c=0,试求函数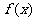 的单调区间;
的单调区间;
(2)若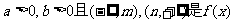 的单调递增区间,试求
的单调递增区间,试求 的范围。
的范围。
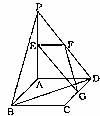
20.(本小题满分12分)如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2;E、F、G分别是线段PA、PD、CD的中点。
(1)求证:PB//平面EFG;
(2)求异面直线:EG与BD所成的角;
(3)在线段CD上是否存在一点Q,使得A到平面EFQ的距离为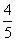 ,若存在,求出CQ的值;若不存在,请说明理由。
,若存在,求出CQ的值;若不存在,请说明理由。
19.(本小题满分12分)
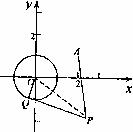
如图,已知圆O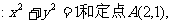 由圆O外一点P(a,b)向圆O引切线PQ,切点为QH满足|PQ|=|PA|。
由圆O外一点P(a,b)向圆O引切线PQ,切点为QH满足|PQ|=|PA|。
(1)求实数a、b间满足的等量关系;
(2)求线段PQ长的最小值;
(3)若以P为圆心所作的圆P与圆O有公共点时,试法语半径最小时,圆P的方程。
18.(本小题满分12分)
根据调查,某学校有30%的学生带了生物书,有60%的学生带了物理书,有10%的学生同时带了生物书和物理书,现从该学校任取3个学生。
(1)求这3个学生中恰好有2个学生带了生物书和概率;
(2)求这3个学生中至多有2个学生带了物理书的概率;
(3)求这3个学生中恰好有1个学生生物书、物理书都没带的概率。
17.(本题满分12分)
若函数f(x)=sinx2ax-sinaxcosax(a>0)的图象与直线y=m相切,并且切点的横坐标依次成公差为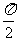 的等差数列
的等差数列
(1)求a和m的值
(2) 若点A(x0,y0)是y=f(x)图像的对称中心,且x0∈[0,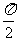 ],求点A的坐标
],求点A的坐标
16.将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论:
①AC⊥BD; ②ACD是等边三角形;
③AB与平面BCD所成的角为60°; ④△AB与CD所成的角为60°
其中正确的序号是 .(写出你认为正确的结论的序号)
15.设数列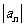 为公比 q>1的等比数列,若a4,a5是方程4x2-8x+3=0的两根,则a6+a7= .
为公比 q>1的等比数列,若a4,a5是方程4x2-8x+3=0的两根,则a6+a7= .
14.两个正数m,n的等差中项是5,等比中项是4。若m>n,则椭圆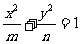 的离心率e的大小为
.
的离心率e的大小为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com