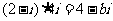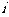1．若(其中是虚数单位，b是实数)，则b=　　　　　　　　　　　　　　 (　　 )

A．-4　　　　　　　　　　　 B．4　　　　　　　　　　　　 C．-8　　　　　　　　　　　 D．8

22．选做题。(本小题满分10分。请考生在A、B、C三题中任选一题作答，如果多做，则按所做的第一题记分．作答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑．)

A．(几何证明选讲选做题)

自圆O外一点P引切线与圆切于点A，M为PA中点，过M引割线交圆于B,C两点．

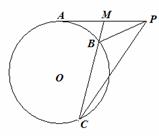
求证:∠MCP=∠MPB．

B．(坐标系与参数方程选做题)

已知椭圆C的极坐标方程为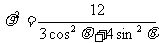，点F₁、F₂为其左，右焦点，直线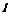的参数方程为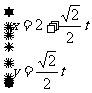(t为参数，t∈R)．

　 (Ⅰ)求直线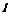和曲线C的普通方程；

　 (Ⅱ)求点F₁、F₂到直线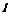的距离之和.

C．(不等式选讲选做题)

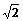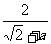设a∈R且a≠-,比较与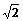-a的大小．

21．(本小题满分12分)

已知椭圆C: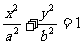(a＞b＞0)，点F₁、F₂分别是椭圆的左、右焦点，点P(2,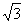)在直线x=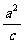上，且|F₁F₂|=|PF₂|,直线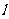:y=kx+m为动直线，且直线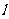与椭圆C交于不同的两点A、B。

　 (Ⅰ)求椭圆C的方程；

　 (Ⅱ)若在椭圆C上存在点Q，满足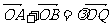(O为坐标原点)，求实数的取值范围；

(Ⅲ)在(Ⅱ)的条件下，当取何值时，△ABO的面积最大，并求出这个最大值．

20．(本小题满分12分)

　　 已知函数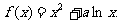

　 (I)当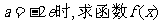的单调区间和极值；

　 (II)若函数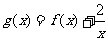在[1，4]上是减函数，求实数a的取值范围.

19．(本小题满分12分)

某电视台举行电视奥运知识大奖赛，比赛分初赛和决赛两部分．为了增加节目的趣味性，初赛采用选手选一题答一题的方式进行，每位选手最多有5次选题答题的机会，选手累计答对3题或答错3题即终止其初赛的比赛，答对3题者直接进入决赛，答错3题者则被淘汰．已知选手甲答题的正确率为．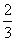

　 (Ⅰ)求选手甲可进入决赛的概率；

　 (Ⅱ)设选手甲在初赛中答题的个数为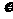，试写出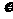的分布列，并求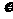的数学期望．

18．(本小题共12分)

在三棱锥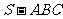中，，.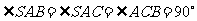

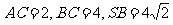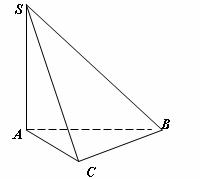
　 (Ⅰ)证明：⊥；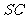

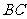　 (Ⅱ)求二面角A-BC-S的大小；

　 (Ⅲ)求直线AB与平面SBC所成角的正弦值.

17．(本小题满分12分)

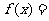
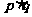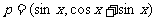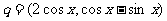设函数,其中向量, ,x∈R.

　 (I)求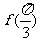的值及函数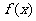的最大值；

　 (II)求函数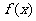的单调递增区间.

16．观察下列不等式：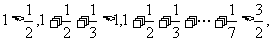

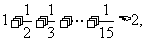
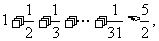
，由此猜想第n个不等式为____.

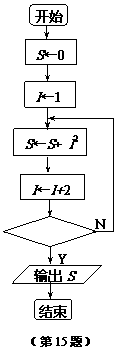
15．下面的流程图可以计算的值，则在判断框中可以填写的表达式为　　 .

14．设向量a=(1,x),b=(2,1-x)，若a·b<0，则实数x的取值范围是　　　　　 。